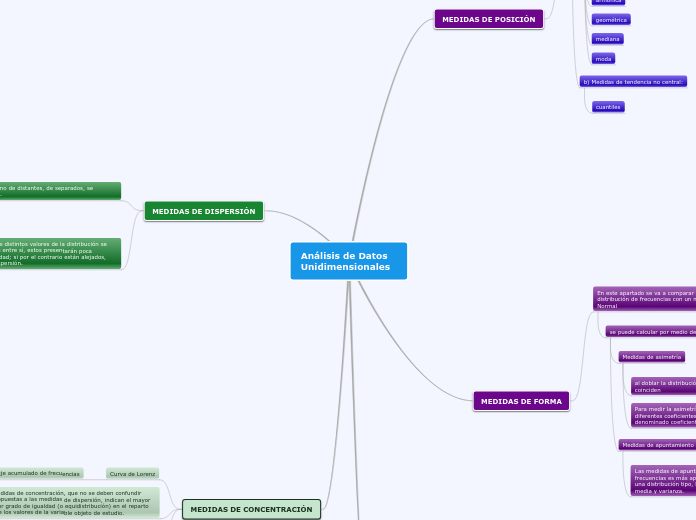
Análisis de Datos Unidimensionales

En general, las medidas de posición indican un valor de la variable en torno al cual se sitúan un grupo de observaciones. Puede distinguirse entre:

a) Medidas de tendencia central:

media aritmética

armónica

geométrica

mediana

moda

b) Medidas de tendencia no central:

cuantiles

En este apartado se va a comparar una determinada distribución de frecuencias con un modelo ideal, la distribución Normal

se puede calcular por medio de:

Medidas de asimetría

al doblar la distribución por el eje de simetría ambas partes coinciden

Para medir la asimetría de una distribución pueden utilizarse diferentes coeficientes, aunque es frecuente obtener el denominado coeficiente de asimetría (de Fisher)

Medidas de apuntamiento (curtosis)

Las medidas de apuntamiento analizan si una distribución de frecuencias es más apuntada o menos al comparar ésta con una distribución tipo, la distribución Normal con su misma media y varianza.

Supóngase que, en principio, se está trabajando con la distribución de frecuencias de una variable estadística X, de la que se ha obtenido una serie de estadísticos (media, varianza, etc,) y que por cualquier circunstancia es necesario pasar a trabajar con otra variable estadística Y, que se obtiene a partir de la anterior como resultado de:

Sumar (o restar) una constante a a todos los valores de la variable estadística X, es decir, de efectuar sobre ésta un cambio de origen

Y = X + a o Y = X - a.

Multiplicar (o dividir) por una constante b todos los valores de la variable X, es decir, de realizar sobre X un cambio de unidad (o escala):

Y = b · X o

Practicar sobre la variable X tanto un cambio de unidad como de origen

Y = b · X + a.

hace referencia a cómo de distantes, de separados, se encuentran los datos.

Rango

SubtoEl rango o recorrido de una distribución es la diferencia entre el valor máximo y mínimopic

Varianza y desviación típica

la media aritmética de los cuadrados de las diferencias de los valores de la variable a la media aritméticaic

Coeficiente de variación de Pearson

Es el cociente entre la desviación típica y la media aritmética de la variable estadística X. Suele representarse por g0(X).

En este sentido, si los distintos valores de la distribución se encuentran próximos entre sí, estos presentarán poca dispersión o variabilidad; si por el contrario están alejados, mostrarán mucha dispersión.

Curva de Lorenz

e relaciona el porcentaje acumulado de frecuencias

Las medidas de concentración, que no se deben confundir como opuestas a las medidas de dispersión, indican el mayor o menor grado de igualdad (o equidistribución) en el reparto total de los valores de la variable objeto de estudio.

Índice de Gini

El índice de Gini, que se denota por IG, es aproximadamente el cociente entre el área comprendida entre la bisectriz del primer cuadrante y la curva de Lorenz y el triángulo