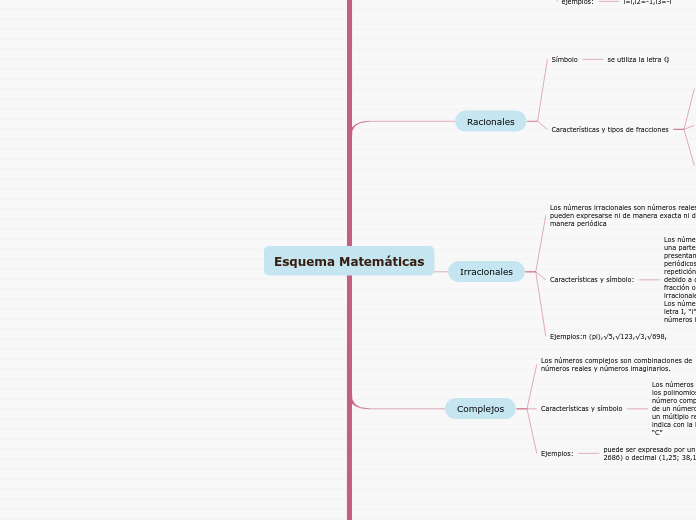
Esquema Matemáticas

Los números naturales son aquellos que nos permiten contar los elementos de un conjunto

Características y símbolo:

Siguen un orden creciente

Son infinitos, sin embargo los números entre uno natural y otro, son finitos y no son considerados naturales.

Se representan con la letra N

Ejemplos:

1, 2, 3, 4, 5, 6 ,7, 8, 9, 10, ...

Los números enteros son cualquier número que corresponda al conjunto de los números naturales más sus opuestos incluyendo el número cero

Características y símbolo:

No tienen una parte decimal

Se representan con la letra Z

Propiedades:

Al realizar operaciones como suma, resta, multiplicación y división, el signo de los números que cual utilizaremos, son los que definen qué signo tendrá el resultado

Ejemplos:

28, -6, 900, -78

Los números reales son cualquier número que corresponda a un punto en la recta real y pueden clasificarse en números naturales, enteros, racionales e irracionales
el conjunto de los números reales (denotado por R)

los subconjuntos: Todos los racionales son algebraicos y los irracionales pueden ser algebraicos y trascendentes.

Ejemplos: : e, π (pi), √2, -√2, √3, -√5, 1/3, -2/5, 8/7, 1, -4, 0, 5

los números imaginarios son números complejos y pueden escribirse como la multiplicación de la unidad imaginaria i por un número real cualquiera. Se utiliza la i para denotar la unidad imaginaria dado que proviene del inglés, imaginary numbers

Características y símbolo: Durante la sustracción, por cada número imaginario, existe un número negativo cuya adición dará como resultado cero. ... Existe un número neutro que al ser sumado a cualquier número, el resultado será el mismo número

ejemplos:

i=i,i2=-1,i3=-i

Símbolo

se utiliza la letra ℚ

Características y tipos de fracciones

Fracciones quebrados: son una forma de expresar una fracción indicando la cantidad de partes en que ha sido dividida, y la cantidad de esas partes que se toma en consideración

Decimales finitos: son aquellos que tienen fin, es decir, no hay un número que se repita. Ejemplos: 4,56 ; 0,0003 ; 2,9876 : 0,1 ; 3,42 , etc.

Decimal periódico: Un número decimal es periódico puro si su parte decimal está formada por uno o varios números que se repiten indefinidamente. Ejemplo, el número 3,23232323. es un decimal periódico puro con periodo 23.

Los números irracionales son números reales que no pueden expresarse ni de manera exacta ni de manera periódica

Características y símbolo:

Los números irracionales son aquellos que tienen una parte decimal de números infinitos y no presentan un número o grupo de números periódicos, en otras palabras, no existe una repetición en la parte decimal. Se le llama irracional debido a que no es posible expresar en forma de fracción o de razón, a diferencia de los números irracionales que se pueden expresar como fracciones
Los números irracionales son presentados por la letra I, “i” mayúscula. Otra forma de presentar los números irracionales es R – Q

Ejemplos:π (pi),√5,√123,√3,√698,

Los números complejos son combinaciones de números reales y números imaginarios.

Características y símbolo

Los números complejos incluyen todas las raíces de los polinomios, a diferencia de los reales. Todo número complejo puede representarse como la suma de un número real y un número imaginario (que es un múltiplo real de la unidad imaginaria, que se indica con la letra i, o en forma polar). su simbolo es “C”

Ejemplos:

puede ser expresado por un número entero (4, 15, 2686) o decimal (1,25; 38,1236; 29854,152).

¿Qué es?

El máximo común divisor (MCD) es el mayor número por el cual se pueden dividir dos o más números. Sin dejar ningún residuo. Un divisor puede definirse formalmente como aquel número que está contenido en otro de forma exacta una cantidad n de veces.

Características donde utilizar

Utilizaremos el M.C.D. en aquellos problemas que nos pidan “dividir o repartir en partes iguales”, “hacer grupos” o nos pregunten por “el máximo, el mayor, el más grande, el más amplio”

Ejemplo

¿Qué es?

El mínimo común múltiplo (mcm) es el número positivo más pequeño que es múltiplo de dos o más números.Los múltiplos de un número son los que obtienes cuando lo multiplicas por otros números.El mínimo común múltiplo es el número más pequeño de los múltiplos comunes.

Características donde utilizar

En un problema habrá que usar el m.c.m. cuando nos pregunten por “algo que se repite en el tiempo”, cuando nos pregunten por el momento en el que “se vaya a coincidir” o cuándo “se encuentran”. Lo que tenemos que calcular será siempre un número mayor o igual a los números dados en el problema.

Ejemplo

Subtopic

Definición de números naturales — Definicion.de. (s. f.). Definición.de. Recuperado 18 de agosto de 2021, de https://definicion.de/numeros-naturales/

Definición de números enteros — Definicion.de. (s. f.). Definición.de. Recuperado 18 de agosto de 2021, de https://definicion.de/numeros-enteros/

Números Imaginarios. (2017, 30 mayo). Números Irracionales. https://numerosirracionales.com/numeros-imaginarios

Rodó, P. (2021, 2 marzo). Números complejos. Economipedia. https://economipedia.com/definiciones/numeros-complejos.html

Rodó, P. (2021b, mayo 10). Números reales. Economipedia. https://economipedia.com/definiciones/numeros-reales.html

CARACTERISTICAS DE LOS NUMEROS ENTEROS - cudrisvirtual. (s. f.). cudrisvirtual. Recuperado 18 de agosto de 2021, de https://sites.google.com/site/cudrisvirtual1/services

de Vega, D. G. (2020, 15 diciembre). Mínimo común múltiplo (mcm): qué es, cómo sacarlo. Smartick. https://www.smartick.es/blog/matematicas/recursos-didacticos/minimo-comun-multiplo-mcm/

L. (2020, 29 septiembre). Ahora que ya sabes calcular el mínimo común múltiplo (m.c.m.) y el Read more. Las clases de Laura. https://www.lasclasesdelaura.com/problemas-de-mcm-y-mcd/

Westreicher, G. (2020, 21 septiembre). Máximo común divisor (MCD). Economipedia. https://economipedia.com/definiciones/maximo-comun-divisor-mcd.html

Fracción generatriz de números decimales (exacto, periódico puro y periódico mixto). (s. f.). Fracción. Recuperado 18 de agosto de 2021, de https://www.matesfacil.com/ESO/fraccion_generatriz/obtener-fraccion-generatriz-numero-decimal-exacto-periodico-puro-mixto.html