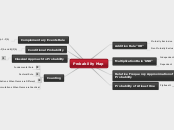
Probability Map
Addition Rule "OR"
Mutually Exclusive
Non Mutually Exclusive
Multiplication Rule "AND"
Independent
Dependent
Relative Frequency Approximation of Probability
P(A)= Number of times A occurred/ number of times the procedure was repeated
Probability of Atleast One
P(atleast 1__)= 1-P(o___)
Complementary Events Rule
P(A) +P(À)= 1, P(A)= 1-P(À), P(À)= 1-P(A)
Conditional Probability
P(B/A)= P(A and B)/P(A)
Classical Approach to Probability
s/n
Counting
Fundamental Rule
Factoral Rule
Permutations When Items are Different
Permutations When Items are Identical
Combinations Rule