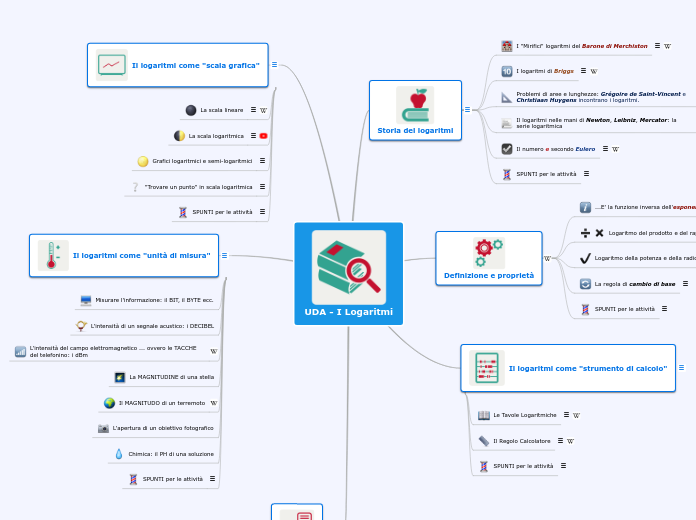
UDA - I Logaritmi

...

John Napier, nobiluomo scozzese che si diletta di matematica, propone nel 1614 i suoi logaritmi come strumento per facilitare le moltiplicazioni.Fontehttps://it.wikipedia.org/wiki/Nepero

Henry Briggs, venuto a conoscenza dei logaritmi di Nepero, sostiene l'uso della base 10.Stende le prime tavole logaritmiche in questa base.Fontehttps://it.wikipedia.org/wiki/Henry_Briggs

Il gesuita fiammingo Grégoire de Saint-Vincent riconosce la natura logaritmica dell'area sottesa dall'iperbole equilatera.Poco dopo l'olandese Christiaan Huygens nota che il problema della rettificazione della parabola si riconduce alla quadratura dell'iperbole. Anche la lunghezza dell'arco di parabola è, quindi, di natura logaritmica.FonteCarl Boyer, Storia della Matematica, Mondadori.

Con l'invenzione dell'analisi da parte di Newton e Leibniz vengono dati gli sviluppi in serie delle funzioni elementari.Talvolta si "riscoprono" serie già note come la serie di James Gregory per il numero pi-greco e la serie logaritmica trovata da Mercator.Fontihttps://it.wikipedia.org/wiki/Formula_di_Leibniz_per_pihttps://it.wikipedia.org/wiki/Serie_di_Mercator

Leonhard Euler indica con la lettera e la base dei logaritmi naturali, definita comee=\lim_{n \rightarrow \infty}\left(1+\frac{1}{n}\right)^nQuesta simbologia, come molte altre introdotte dal matematico svizzero, rimarrà standard.Fontehttps://it.wikipedia.org/wiki/E_(costante_matematica)

Gli studenti eseguono ricerche di gruppo sui personaggio citati.Inquadrano lo stato delle discipline matematiche del periodo di interesse.Raccolgono le informazioni in elaborati multimediali.

Sea^x=yallora diciamo chex=\log_{a}{y}Fontehttps://it.wikipedia.org/wiki/Logaritmo

Il logaritmo trasforma prodotti in somme e rapporti in differenze....

Si può portare fuori dal logaritmo l'esponente di una potenza...

Il logaritmo in una base è proporzionale al logaritmo in un'altra base...

Gli studenti organizzano tavole grafiche con le proprietà dei logaritmi.Illustrano esempi con numeri semplici.Acquisiscono abilità nell'editing al computer di formule matematiche.

Dalle origini fino a tempi non lontani (anni '70) i logaritmi avevano una importanza pratica nella facilitazione dei calcoli manuali.Con l'avvento degli strumenti di calcolo digitale questi aspetti sono divenuti esclusivamente di interesse storico.

Una TAVOLA LOGARITMICA è un volume stampato che elenca i valori dei logaritmi di una serie di numeri consecutivi, con una certa precisione (ad es. dieci cifre decimali).Usando una tavola e le proprietà dei logaritmi le moltiplicazioni, divisioni, potenze e radici risultano molto facilitate.Fontehttps://en.wikipedia.org/wiki/Mathematical_table

Un REGOLO CALCOLATORE è uno strumento meccanico formato da due scale graduate "logaritmicamente" che scorrono l'una sull'altra.La loro posizione reciproca permette di effettuare meccanicamente una moltiplicazione.Fontehttps://it.wikipedia.org/wiki/Regolo_calcolatore

Gli studenti realizzano un semplice regolo calcolatore in cartone o legno o plastica.

Nella scienza e nella tecnica occorre talvolta rappresentare su un asse valori che coprono diversi ordini di grandezza. Ad esempio: 1, 10, 100, 1000.La scala lineare in questi casi non è adeguata.Scale basate sui logaritmi forniscono la soluzione.

Ordinariamente un grafico è tracciato in scala lineare: lo stesso spostamento lungo un asse corrisponde alla stessa variazione della variabile.

Lungo un asse in scala logaritmica lo stesso spostamento corrisponde alla moltiplicazione per uno stesso fattore della variabile.

Un grafico è in scala logaritmica se ambedue gli assi (ascisse ed ordinate) sono in scala logaritmica.E' in scala semi-logaritmica se uno dei due assi è logaritmico e l'altro è lineare.

Le proprietà dei logaritmi stabiliscono con esattezza il valore di ogni punto preso su un asse logaritmico, una volta stabilita la posizione di due valori, ad esempio 1 e 10.Come per la scala lineare, non ci sono margini di ambiguità.

Gli studenti sono invitati a raccogliere e commentare esempi di grafici in scala lineare, semilogaritmica e logaritmica, realizzando degli elaborati illustrativi di tipo grafico e testuale.

Alcune unità di misura sono intrinsecamente di tipo logaritmico.Questo rende più pratico l'uso dei valori, che altrimenti sarebbero numeri estremamente grandi o estremamente piccoli.

Gli studenti raccolgono link (volutamente assenti nella mappa) e informazioni di base su ognuna delle unità di misura citate nella mappa.Approfondiscono il significato di una unità di misura logaritmica che interviene in una materia specialistica del loro corso di studi.Realizzano delle esperienze di misura, raccolta dati, stesura di tabelle, elaborazione di grafici sotto il coordinamento del docente della materia specialistica.

Verifica finale con un quiz a risposte sia chiuse che aperte.Strumento: Google Moduli