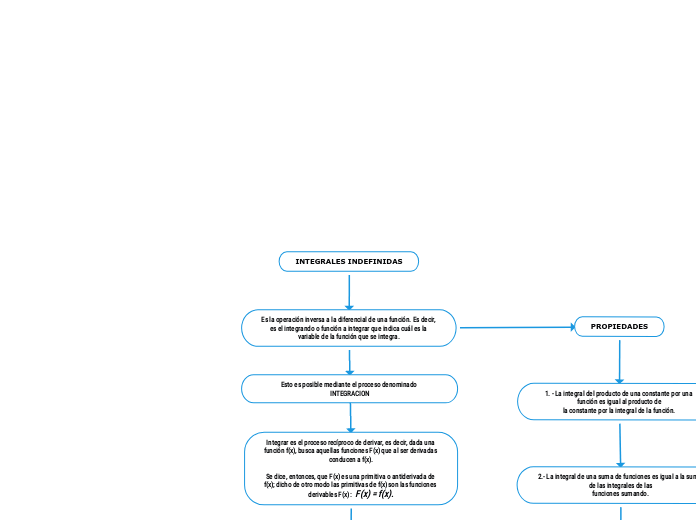
INTEGRALES INDEFINIDAS
Es la operación inversa a la diferencial de una función. Es decir, es el integrando o función a integrar que indica cuál es la variable de la función que se integra.
Esto es posible mediante el proceso denominado INTEGRACION
Integrar es el proceso recíproco de derivar, es decir, dada una función f(x), busca aquellas funciones F(x) que al ser derivadas conducen a f(x).
Se dice, entonces, que F(x) es una primitiva o antiderivada de f(x); dicho de otro modo las primitivas de f(x) son las funciones derivables F(x) : F(x) = f(x).
Si una función f(x) tiene primitiva, tiene infinitas primitivas, diferenciándose todas ellas en una constante. La integral indefinida se representa por: ∫ f (x)dx
PROPIEDADES
1. - La integral del producto de una constante por una función es igual al producto de
la constante por la integral de la función.
∫c ⋅ f (x) dx = c ⋅∫ f (x)dx
2.- La integral de una suma de funciones es igual a la suma de las integrales de las
funciones sumando.
∫[ƒ(x) + g(x)] dx = ∫ƒ(x) dx + ∫g(x) dx
3.- la integral de una diferencia de funciones es igual a la diferencia de las
integrales de las funciones minuendo y sustraendo.
∫[ƒ(x) - g(x)] dx = ∫ƒ(x) dx - ∫g(x) dx
4.- Como consecuencia de las dos propiedades anteriores:
La integral de una suma algebraica de funciones es igual a la suma algebraica
de las integrales de todas y cada una de las funciones sumandos.
∫(x − x + )dx = ∫x dx − ∫x dx + ∫dx = x3/3 - x2/2 | x + c