Geometric/Measurement

Geometric Figures

Prisms: a prism is a polyhedron in which two congruent faces "the bases" lie in parallel planes and the other faces (lateral faces) are bounded by parallelograms

Hexagonal oblique prism

Hexagonal oblique prism

Triangular Right Prism

Triangular Right Prism

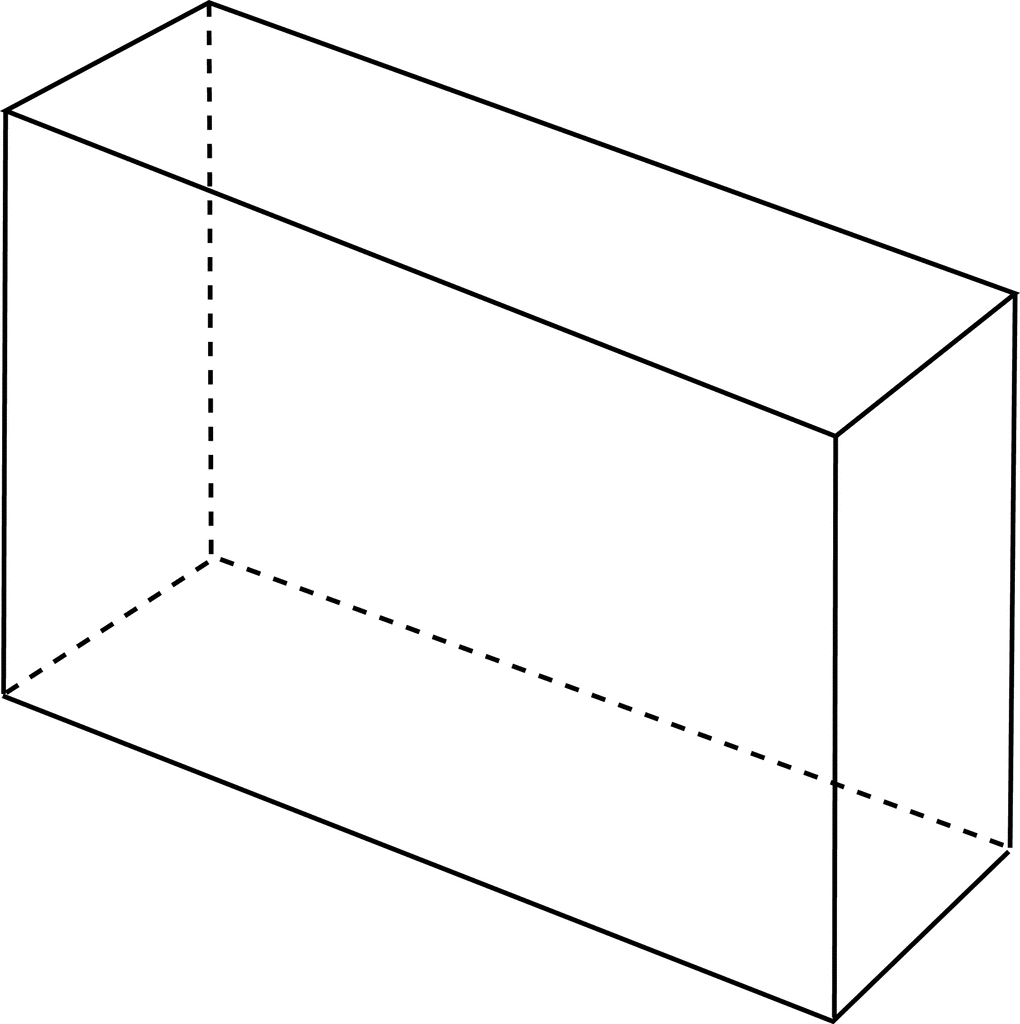
Quadrilateral Right Prism

Quadrilateral Right Prism

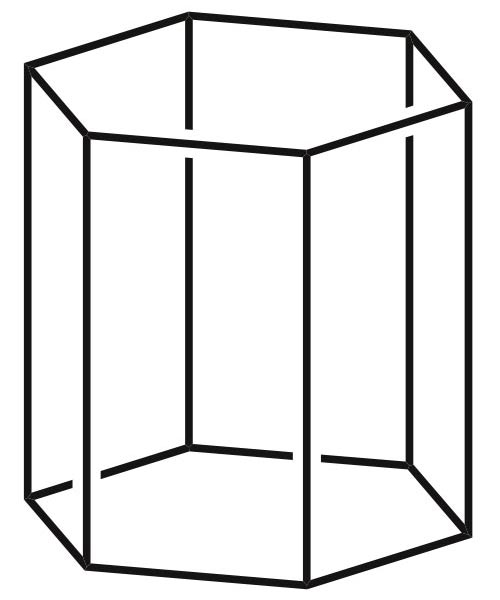
Hexagonal Right Prism

Hexagonal Right Prism

Right Pyramids:

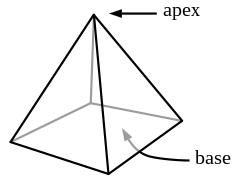
Triangular Pyramid

Triangular Pyramid

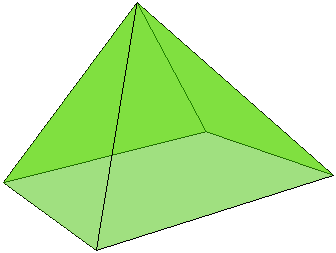
Square Pyramid

Square Pyramid

Cylinders: A simple closed surface that is not a polyhedron

Cylinders: A simple closed surface that is not a polyhedron

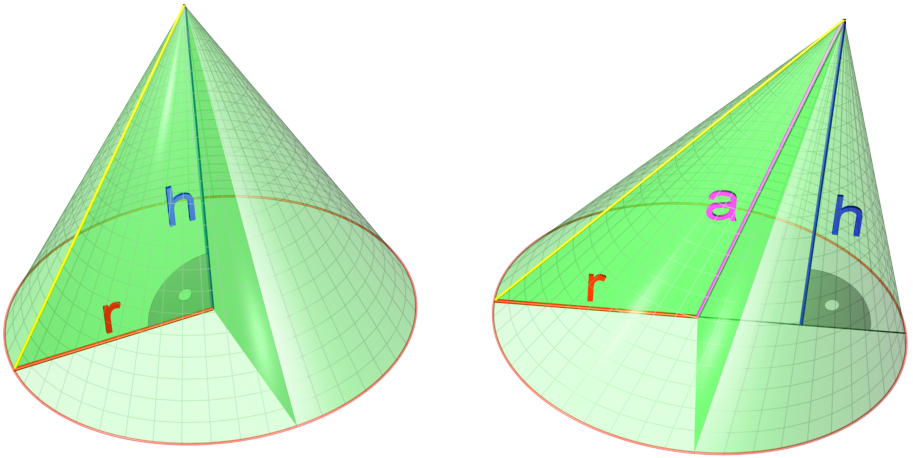
Cones: The union of the line segments connecting a point P with each point of a simple, closed curve, the simple, closed curv

Cones: The union of the line segments connecting a point P with each point of a simple, closed curve, the simple, closed curve in the interior of the group

Classifications of Polygons:

Polygon: all sides are congruent and all angles are congruent

Right triangle: a triangle in which all the angles are acute.

Acute triangle: a triangle in which all the angles are acute

Obtuse triangle: a triangle containing one obtuse angle

Scalene triangle: triangle with no congruent sides

Isosceles triangle: a triangle with at least two congruent sides.

Kitequadrilateral with two adjacent sides congruent and the other two sides are also congruent.

Trapezoid: a quadrilateral with at least one pair of parallel sides.

Isosceles trapezoid: a trapezoid with congruent base angles.

Parallelogram: a quadrilateral in which each pair of opposite sides are parallel.

Rectangle: a parallelogram with a right angle.

Supplementary: the sum of the measure of two angles is 180 Complimentary angles: the sum of the measures of two complementary angles is 90 degrees Congruent angles: all angles are the same Vertical angles: a pair of angles whose sides are two pairs of opposite rays Corresponding angles: have the same angle measures in degrees Classification of angles: types of angles include acute, obtuse, right and straight angle. Angles can also be adjacent or vertical Angle: a figure formed by two rays

Area and Perimeter

Length=8 Width=4 LW=32cm2

Length=8 Width=4 LW=32cm2

Base=2 Height=5 BH=10u2

Base=2 Height=5 BH=10u2

Base=4 Height=5 BH1/2=10u2

Base=4 Height=5 BH1/2=10u2

Base1=3 Base2=5 Height=4 1/2(b1+b2)h=16u2

Base1=3 Base2=5 Height=4 1/2(b1+b2)h=16u2

Radius=R

Diameter=D

Pi=3.14

D=6 Pi=3.14 C=18.84u

D=6 Pi=3.14 C=18.84u

R=3 Pi=3.14 A=28.26u2

R=3 Pi=3.14 A=28.26u2

Surface Area

Surface area of Prism 2(base x height) + 2(length x base) + 2(length x height) When doing a triangular prism it is half of t

Surface area of Prism
2(base x height) + 2(length x base) + 2(length x height)

When doing a triangular prism it is half of the formula

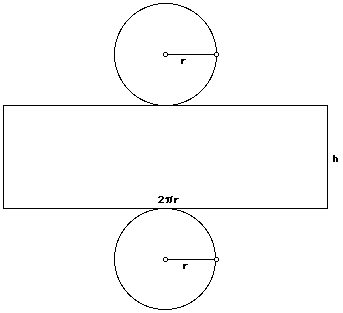
Surface area of Cylinder 2πr² + 2πrh When sliced you must add the surface area of the side it is sliced on

Surface area of Cylinder
2πr² + 2πrh

When sliced you must add the surface area
of the side it is sliced on

Surface area of pyramid area of base x 2(base x slanted height)

Surface area of pyramid
area of base x 2(base x slanted height)

Surface area of Cone πr² + πrs

Surface area of Cone
πr² + πrs<slanted height

Surface area of sphere 4πr² for a hemisphere you must add the face it looks sliced on

Surface area of sphere
4πr²

for a hemisphere you must add the face it looks sliced on

Pythagorean Theorem

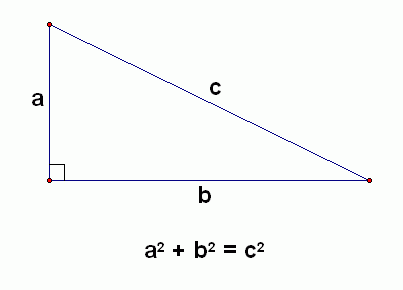
a² + b² = c² Only works for right triangles Atleast one angle must be 90 degrees If.. a² + b² ≠ c² then it is not a right tr

a² + b² = c²
Only works for right triangles
Atleast one angle must be 90 degrees

If.. a² + b² ≠ c² then it is not a right triangle
and pythagorean thereom does not work

Volume

Volume of a Prism Surface area of base x height

Volume of a Prism
Surface area of base x height

Volume of a Triangular Prism ½(surface area of base x height)

Volume of a Triangular Prism
½(surface area of base x height)

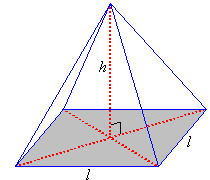
Volume of a Pyramid ⅓(surface area of base x height)

Volume of a Pyramid
⅓(surface area of base x height)

Volume of a Cone ⅓ (πr² x height)

Volume of a Cone
⅓ (πr² x height)

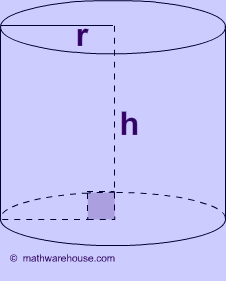
Volume of a Cylinder πr² x height

Volume of a Cylinder
πr² x height

Volume of a Sphere 4/3(πr³)

Volume of a Sphere
4/3(πr³)