Analytic Geometry
Linear Equations
Slope-Intercept
Gives the rate of change
m = multiplier
Steepness of a line
Slope
(x,0)
Graphs line quickly
Gives the initial value
Standard Form
No fractions
x-term first
y-term second
equals to 0
Gives us the x-intercept and y-intercept quickly.
y-intercept

you can find the y-intercept by looking at a what point the line touches the y-axis; point (x,o) OR you can look at the equation of a line. For slope-intercept, y=mx +b, the "b" would be the y-intercept. For standard form, Ax+By+C=0, the "y" would be the y-intercept.
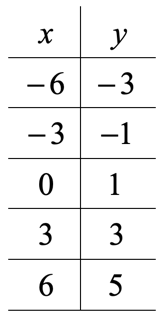
to find the y-intercept in a table of values, you can look at where x is 0. For example, on this table, the y-intercept is 1.
you would need the y-intercept of a line or a graph to figure out if it's a partial variation, or a direct variation.
if the y-intercept = 0, it is a direct variation. if the y-intercept is NOT 0, it is a partial variation.
rate of change
Changes in y-values divided by the changes in the x-values to compare steepness
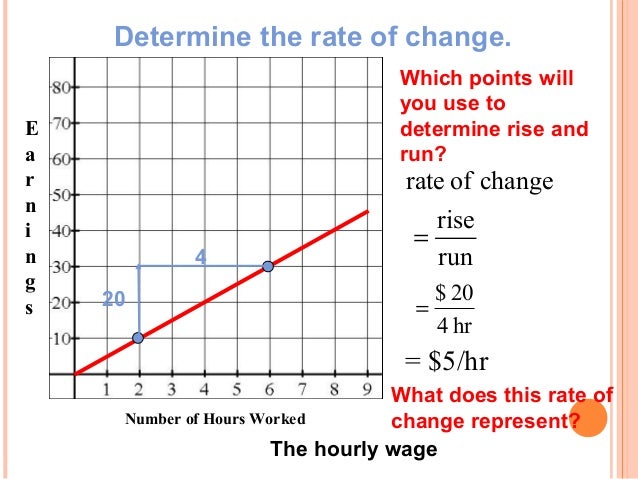
this is an example of rise/run. you divide the rise of a line by its run to get the slope.
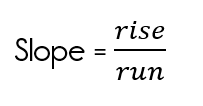
you would need the rate of change to determine the steepness of a line, or how slow or fast a line grows. You can also compare the changes of the x-values with the changes of the y-values.