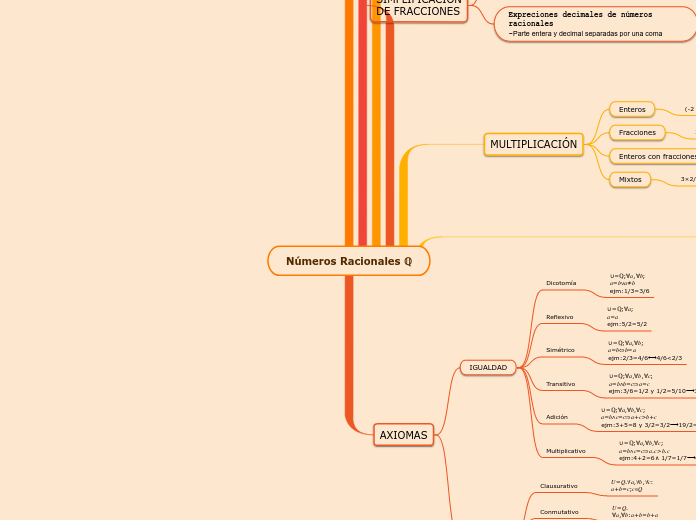
Números Racionales ℚ
RESTA
Se representa simbolicamente de la siguiente manera:𝑈=𝑄.∀𝑎,∀𝑏,∀𝑐:𝑎+𝑏=𝑎+(−𝑏)
SUMA
Fracción con igual denominador
ejm:8/3+5/3=8+5/3=13/3
Fracción con distinto denominador
ejm:3/4+7/10=15+14/20=29/20
Con números mixto
ejm: 2 3/4=2.4+3/4=11/4
Con números enteros y mixtos
ejm: 1+2=3 o 1 1/2+2 3/4
- a/b-->"a" y "b" son enteros, "b"
diferente de cero
- Son subconjunto los números enteros y naturales.
-VALOR ABSOLUTO:I±𝑎I=+𝑎
RACIONALES NO ENTEROS O FRACCIONARIOS
Fracción Propia
-Numerador menor que el denominador. Toda fracción propia es menor que la unidad
Fracción Impropia
-Numerador mayor que el denominador. Toda fracción impropia es mayor que la unidad.
SIMPLIFICACIÓN
DE FRACCIONES
-Convertir la fracción en otra igual a la primera
-Para simplificar se divide el numerador para el denominador por su m.c.d
Expreciones decimales de números racionales
-Parte entera y decimal separadas por una comaundefinedundefined
Tipos de Números decimales
Número Entero
Es división exacta
20/4=5
N. Decimal Exacto
Cifras decimales finitas
ejm: 1/4=0,25
N. Decimal Infinito
Periódico Puro
Infinitas cifras decimales,
a partir de la coma se repiten
ejm:10/3=0.3333=0,3̂
N. Decimal Infinito
Periódico Mixto
Infinitas cifras decimales,
a partir de la coma se repiten
y otras no
ejm:7/18=0,388=0,38̂
MULTIPLICACIÓN
Enteros
(-2 ).(-6)=12
Fracciones
2/3×5/2=2×5/3×2=10/6
Enteros con fracciones
3×2/5=3/1×2/5=3×2/5=6/5
Mixtos
3×2/7×6/5=3/1×2/7×6/5=36/35
LEY DE SIGNOS
(+𝒂)(+𝒃)=(+𝒄)
(+𝒂)(−𝒃)=(−𝒄)
(−𝒂)(+𝒃)=(−𝒄)
(−𝒂)(−𝒃)=(+𝒄)
AXIOMAS
IGUALDAD
Dicotomía
∪=ℚ;∀𝑎,∀𝑏;
𝑎=𝑏∨𝑎≠𝑏
ejm:1/3=3/6
Reflexivo
∪=ℚ;∀𝑎;
𝑎=𝑎
ejm:5/2=5/2
Simétrico
∪=ℚ;∀𝑎,∀𝑏;
𝑎=𝑏⇔𝑏=𝑎
ejm:2/3=4/6⟷4/6<2/3
Transitivo
∪=ℚ;∀𝑎,∀𝑏,∀𝑐;
𝑎=𝑏∧𝑏=𝑐⇒𝑎=𝑐
ejm:3/6=1/2 y 1/2=5/10⟶3/6=5/10
Adición
∪=ℚ;∀𝑎,∀𝑏,∀𝑐;
𝑎=𝑏∧𝑐=𝑐⇒𝑎+𝑐>𝑏+𝑐
ejm:3+5=8 y 3/2=3/2⟶19/2=19/2
Multiplicativo
∪=ℚ;∀𝑎,∀𝑏,∀𝑐;
𝑎=𝑏∧𝑐=𝑐⇒𝑎.𝑐>𝑏.𝑐
ejm:4+2=6∧ 1/7=1/7⟶6/7=6/7
ADICIÓN
Clausurativo
𝑈=𝑄.∀𝑎,∀𝑏,∀𝑐:
𝑎+𝑏=𝑐;𝑐∈𝑄
Conmutativo
𝑈=𝑄.
∀𝑎,∀𝑏:𝑎+𝑏=𝑏+𝑎
Asociativo
𝑈=𝑄.∀𝑎,∀𝑏,∀𝑐:
(𝑎+𝑏)+𝑐=𝑎+(𝑏+𝑐)
Modulativo
𝑈=𝑄.∀𝑎,𝑆0
𝑎+0=0+𝑎=𝑎
Invertivo
𝑈=𝑄.∀𝑎,∃−𝑎:
𝑎+(−𝑎)=𝑎;𝑎≠0