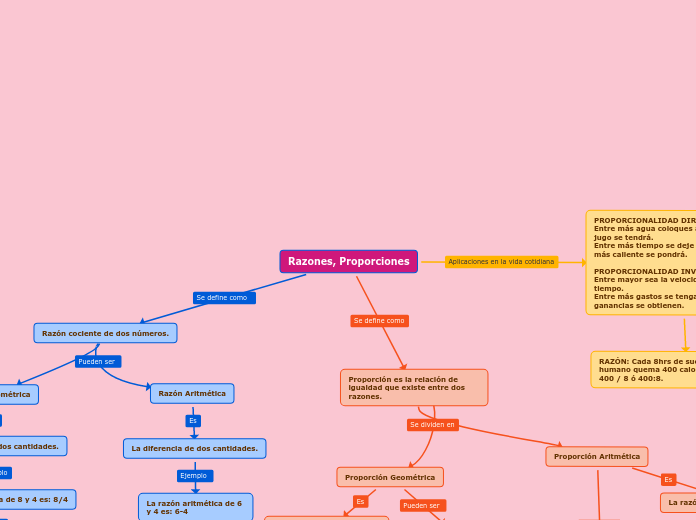
Razones, Proporciones
Razón cociente de dos números.
Razón Aritmética
La diferencia de dos cantidades.
La razón aritmética de 6 y 4 es: 6-4
6 es el antecedente 4 es el consecuente
Razón Geométrica
Es el cociente de dos cantidades.
La razón geométrica de 8 y 4 es: 8/4
8 es el antecedente 4 es el consecuente
Proporción es la relación de igualdad que existe entre dos razones.
Proporción Geométrica
La razón de dos razones geométricas.
1/2 = 3/6
1 y 6 son extremos 2 y 3 son medios
Discretas: Cuando sus medios no son iguales. Ejemplo: 1/3=4/12. Continuas: Cuando sus medios son iguales. Ejemplo: 1/4=4/16
Proporción Aritmética
La razón de dos razones aritméticas.
9-7= 10-8
9 y 8 son extremos 7 y 10 son medios
Discretas: Cuando sus medios no son iguales. Ejemplo: 15-10=12-7. Continuas: Cuando sus medios son iguales. Ejemplos: 28- 21= 21-14
PROPORCIONALIDAD DIRECTA:
Entre más agua coloques a un jugo más jugo se tendrá.
Entre más tiempo se deje en el Sol un metal más caliente se pondrá.
PROPORCIONALIDAD INVERSA:
Entre mayor sea la velocidad menor será el tiempo.
Entre más gastos se tengan menos ganancias se obtienen.
RAZÓN: Cada 8hrs de sueño, el cuerpo humano quema 400 calorías; la razón es 400 / 8 ó 400:8.