FUNCIONES Y RELACIONES
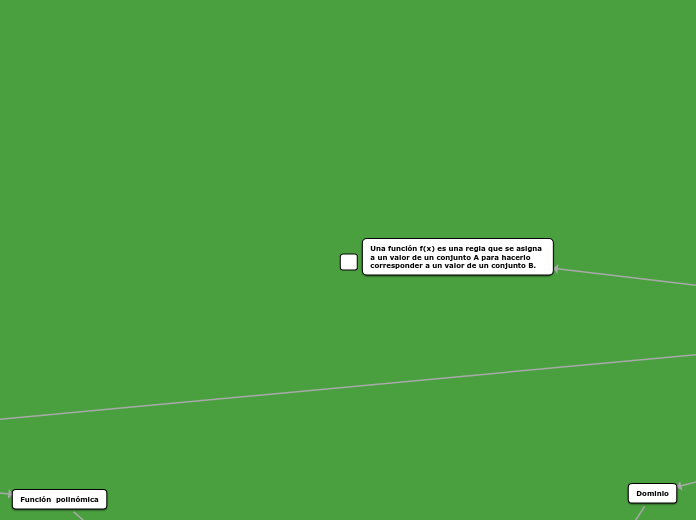
Una función f(x) es una regla que se asigna a un valor de un conjunto A para hacerlo corresponder a un valor de un conjunto B.
Tipos de funciones
Función polinómica
La función polinomica f una función expresada por medio de un polinomio tal y como su nombre lo dice: f(x) = (x-2)^2(x-3) Su dominio son los números reales, y en su dominio son continuas.
Función de primer grado
Las funciones de primer grado son aquellas que tienen un polinomio de grado 1 y están compuestas por una variable independiente que es multiplicada por una escalar
Funciones afines: Son aquellas funciones polinomicas de primer grado que no pasan por el punto (0,0) f(x) = mx + n
Funcionares lineales: Son aquellas funciones polinomicas que pasan por el punto (0,0)y su expresión f(x) = x

Función de identidad: Es aquella que refleja un conjunto M en si mismo
Función cuadrática

Funciones cuadráticas "segundo grado" son funciones polinomicas de grado 2 (x) = ax^2+bx+c
Función cubica

Funcion cubica son funciones polinomicas de grado 3 f(x) 0 ax^(3)+bx^(2)+cx+d
Función racional
las funciones f(x) son el cociente o división de 2 polígonos f(x) g(x)/q(x) su dominio sin todos los números reales execto los valores de la variable X es decir las raíces del polinomio respecto al denominador
Función proporcional inversa: Su dominio son los números reales sin las axintotas y tiene un punto de ruptura y es decreciente
Función radical
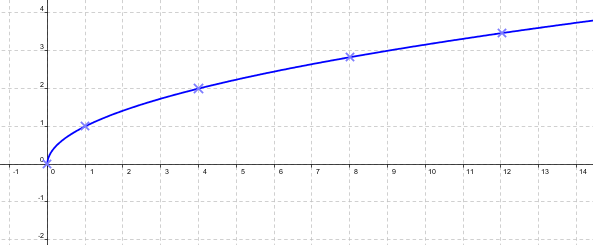
Mejor conocida como función raíz y se obtiene de una variable independiente X a través de una radicacion pero a la hora de radicar su indice debe ser impar y su dominio son los números reales
Funciones trascendentes
Función exponencial: Es aquella que cuenta con una variable x y un base constante a
Función logarítmica: Formada por un logaritmo de base a siendo a diferente y mayo al numero cero
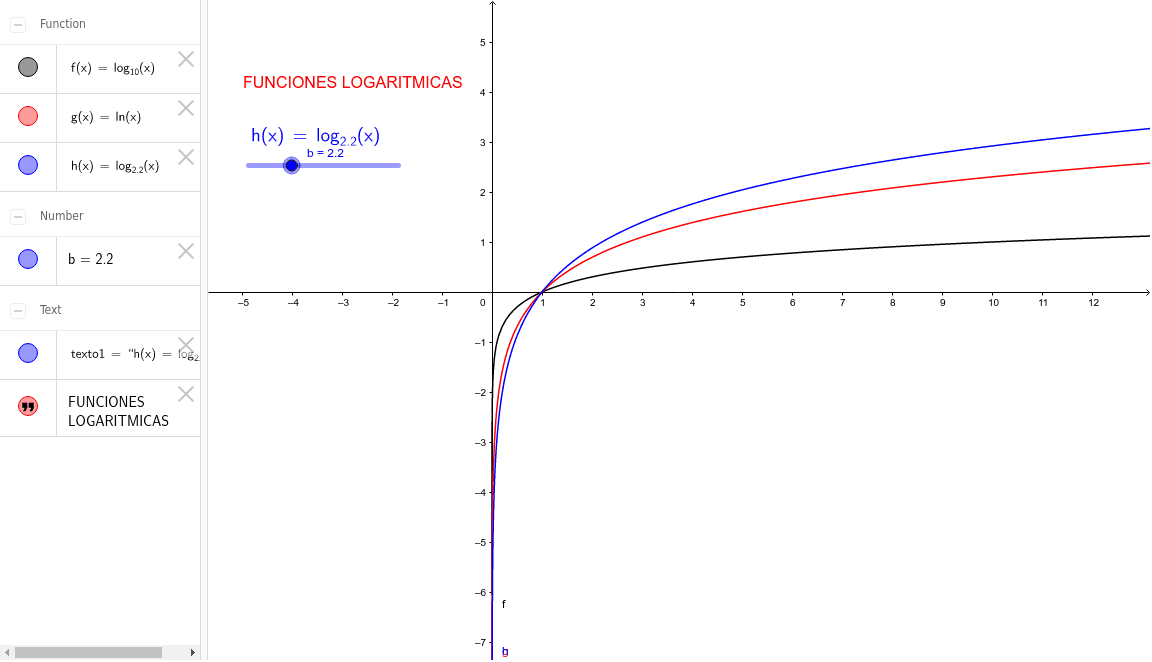
Logarítmica
Funciones trigonométricas:Son funciones que se adoptaron para poder hacer una definición mucho mas grande y diversa de las razones trigonométricas
Funciones definidas a trozos
Mejor conocida como función por partes tiene distintas formas de ser llevada a través de una formula. Y tiene diversas formas de correspondencia dependiendo de la variable independiente, cada trozo puede recibir el nombre de intervalo y un ejemplo de su formulación puede ser así
Funciones inyectivas, sobreyecticas y biyectivas
Este tipo de funciones dan un informe sobre las relaciones que se tienen entre el conjunto de salida X y un conjunto de llegada Y
Funciones explícita e implícitas
funciones implícitas: Es aquella donde la variable dependiente no esta despejada
Funciones Explicitas: Es aquella donde la variable dependiente
Función valor absoluto: Su dominio son los números reales y su condominio son los números reales positivos y solo se pueden deslizar de derecha a izquierda por el eje de las x su función es así f (x) = x
Funcion constante
Es aquella cuyo valor de la variable independiente del eje X de una función f(X) = A donde la variable "A" no cambia. Matemáticamente la expresión con la que se define una función constante es: x1 y x2 del dominio tales que x1<x2, se cumple que f(x1) = f(x2).
Características de una función
Dominio
Es el conjunto de partida de una función

Codominio
En matemáticas es el condominio el conjunto de llegada de una función
Crecimiento

Cuando una función F(X) es creciente cuando en el intervalo (a,b) x1, < x2 en pocas palabras este tipo de funciones el valor nunca decrece es decir siempre esta aumentando o se mantiene F(X1) menor o igual a F(X2)
Decrecimiento

Las funciones decrecientes en el intervalo "a,b" F(X1) mayor o igual a F(X2) estas funciones siempre disminuyen o se mantienen en su valor un valor estable
Maximos
Son los valores mas grandes de una función
Minimos
Minimos: Son los valores mas pequeños de una función
Continuidad
La continuidad en una función puede manifestarse cuando técnicamente se dibuja una función sin levantar el lápiz del papel
Discontinuidad
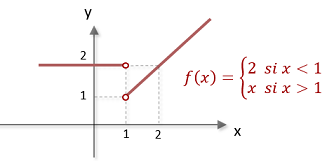
Una función discontinua es aquella que tiene cortes en si misma