Teorema de los límites
2.- Límites Bilaterales
es simplemente un límite en el que los dos límites unilaterales o laterales, o lateral por derecha y lateral por izquierda existen y son iguales
Límite por la derecha
Una función f(x) tiene un límite en a si y solo si tiene límites por la izquierda y por la derecha y estos iguales.
limf(x)=L X →a+
Límite por la izquierda
limf(x)=L X →a+= significa que para todo ∈ >0, existe algún δ >0 tal que, para todo x, si 0 <a-x < δ, entonces I f(x)-L I < ∈.
lim f(x)=L X →a-
Teorema 12
limf(x)=L X →a+= significa que para todo ∈ >0, existe algún δ >0 tal que, para todo x, si 0 <x-a < δ, entonces I f(x)-L I < ∈.
lim f(x)=L X →a- y lim f(x)=L X →a+. Entonces existe el límite: lim f(x)=L X →a y además se cumple que: lim X →a f(x) = lim X →a- f(x) = lim X →a+ f(x)= L
Un límite es cuando nos acercamos a f(x) en un punto.
Los teoremas básicos para determinar el límite de una función en un punto, son los siguientes:
1.- Límites Unilaterales
4.- Límites infinitos
Los límites infinitos son aquellos en los que las imágenes f(x) aumentan o disminuyen sin límite cuando x se aproxima a un valor a.
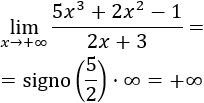
3.- Límites al Infinito
Un límite al infinito es aquel al que tiende f(x) cuando la variable x se hace tan grande, tanto en positivo como en negativo, como queramos. Entonces la función f(x) puede tender a un valor finito o puede diverger a infinito (límite infinito).
lim x → ∞ lim f x ± g x = lim x → ∞ f x ± lim x → ∞ g x = a ± b