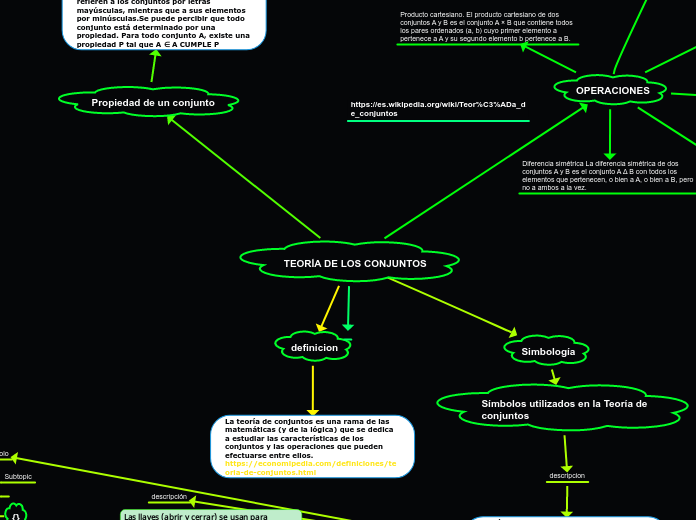
TEORÍA DE LOS CONJUNTOS
definicion
La teoría de conjuntos es una rama de las matemáticas (y de la lógica) que se dedica a estudiar las características de los conjuntos y las operaciones que pueden efectuarse entre ellos. https://economipedia.com/definiciones/teoria-de-conjuntos.html
Simbología
Símbolos utilizados en la Teoría de conjuntos
descripcion
Los símbolos que frecuentemente son utilizados para hablar de conjuntos son los siguientes: para todo (\forall), existe (\exists), igual o identidad (=), variables u objetos individuales (x_1, x_2, x_3, ...). Símbolo de pertenencia (\in), no pertenencia (\not\in). En general la negación particulares símbolos, se identificará con una raya que lo atraviesa desde arriba, hasta abajo, por la mitad.
descripción
simbolo
Subtopic
{}
Propiedad de un conjunto
Una propiedad es una afirmación, que se refiere a la manera en que los objetos que forman un conjunto. Por ejemplo si deseáramos decir que existe un conjunto que tiene un elemento podemos escribir a (a ∈ A ) Denote al conjunto por A (mayúscula) porque varios autores se refieren a los conjuntos por letras mayúsculas, mientras que a sus elementos por minúsculas.Se puede percibir que todo conjunto está determinado por una propiedad. Para todo conjunto A, existe una propiedad P tal que A ∈ A CUMPLE P
OPERACIONES
Unión. La unión de dos conjuntos A y B es el conjunto A ∪ B que contiene cada elemento que está por lo menos en uno de ellos.
Intersección. La intersección de dos conjuntos A y B es el conjunto A ∩ B que contiene todos los elementos comunes de A y B.
Diferencia. La diferencia entre dos conjuntos A y B es el conjunto A \ B que contiene todos los elementos de A que no pertenecen a B.
Complemento. El complemento de un conjunto A es el conjunto A∁ que contiene todos los elementos (respecto de algún conjunto referencial) que no pertenecen a A.
Diferencia simétrica La diferencia simétrica de dos conjuntos A y B es el conjunto A Δ B con todos los elementos que pertenecen, o bien a A, o bien a B, pero no a ambos a la vez.
Producto cartesiano. El producto cartesiano de dos conjuntos A y B es el conjunto A × B que contiene todos los pares ordenados (a, b) cuyo primer elemento a pertenece a A y su segundo elemento b pertenece a B.