Variables Aleatorias

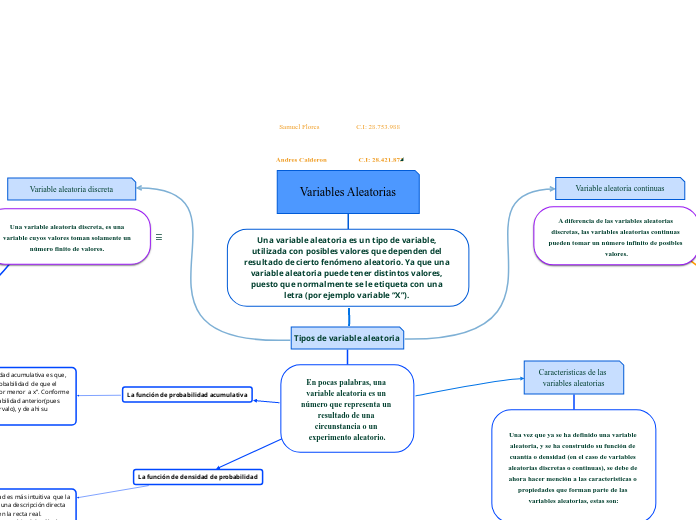
Una variable aleatoria es un tipo de variable, utilizada con posibles valores que dependen del resultado de cierto fenómeno aleatorio. Ya que una variable aleatoria puede tener distintos valores, puesto que normalmente se le etiqueta con una letra (por ejemplo variable “X”).

Tipos de variable aleatoria

En pocas palabras, una variable aleatoria es un número que representa un resultado de una circunstancia o un experimento aleatorio.

La función de probabilidad acumulativa

La premisa de la función de probabilidad acumulativa es que, por definición, FX(x) representa “la probabilidad de que el resultado del experimento sea un valor menor a x”. Conforme x aumentase “acumula” toda la probabilidad anterior(pues está contenida dentro del nuevo intervalo), y de ahi su nombre.

La función de densidad de probabilidad

La función de densidad de probabilidad es más intuitiva que la función acumulativa. Visualmente, es una descripción directa de la distribución de la probabilidad en la recta real. Matemáticamente, es la base para una multitud de cálculos numéricos útiles en el análisis del fenómeno aleatorio.

Variable aleatoria discreta

Una variable aleatoria discreta, es una variable cuyos valores toman solamente un número finito de valores.

Cada valor resultante de una variable aleatoria discreta contiene una cierta probabilidad. En el ejemplo del dado, cada probabilidad de resultado es de 1/6 todo esto gracias a que los valores resultantes son de probabilidades iguales.Otros ejemplos serían:La cantidad de mascotas que tienen las reservas ecologicas en un país La cantidad de panes que se fabrican cada dia en una panaderiaLa cantidad de clientes de una compañia que brinda el servicio de InternetLa cantidad de premios que tiene un autor

Ejemplo

Cuando se lanza un dado, es un evento totalmente aleatorio, pero a su vez, el dado solamente puede tener un número finito de resultados (1, 2, 3, 4, 5 y 6).

Variable aleatoria continuas

A diferencia de las variables aleatorias discretas, las variables aleatorias continuas pueden tomar un número infinito de posibles valores.

Una VA (Variable Aleatoria) es continua si se cumplen las siguientes condiciones1) Su conjunto de valores posibles consiste en todos los números en un solo intervalo en la recta real (por ejemplo, de 0 a +∞) o todos los números en la unión disjunta de intervalos. 2) Ningún valor posible de la variable aleatoria continua tiene probabilidad positiva, es decir, P(X = c) = 0 para cualquier valor de c. Otros ejemplos serían:El valor monetario de las pinturas que hay en un museo.La cantidad de sal que consumen las personas por día.El ancho que tienen los ríos de un bosque.La longitud de avenidas en una ciudad.

ejemplo

las variables que se pueden medir o recolectar de una persona: “Tiempo observado al recorrer una cierta distancia”, “estatura”, “peso”, “nivel de colesterol en sangre”

Caracteristicas de las variables aleatorias

Una vez que ya se ha definido una variable aleatoria, y se ha construido su función de cuantía o densidad (en el caso de variables aleatorias discretas o continuas), se debe de ahora hacer mención a las caracteristicas o propiedades que forman parte de las variables aleatorias, estas son:

Otras medidas: Todas las medidas de centralización, dispersión y forma pueden calcularse sin más que sustituir en aquellas fórmulas la frecuencia relativa por la probabilidad.

Posición: Las medidas de tendencia central (media, mediana o moda) son las que indican el centro de la distribución de frecuencias.

Forma: Las medidas de forma (coeficiente de asimetría o curtosis) logran contrastar la forma que tiene la representacion gráfica, bien sea del historigrama o el diagrama de barras.

Dispersión: Las medidas de dispersión (varianza, desviación típica o coeficiente de variación) son las que cuantifican la separacion, la dispersión y la variabilidad de los valores de la distribución respecto al valor central.

Momento: Dada una variable aleatoria X, se define su momento de orden k(k=0,1,2,...) respecto a la media o momento central de orden k como la esperanza de (X−µ) k

Los momentos son operadores matemáticos que nos proporcionarán información sobre las propiedades de la distribución de la variable aleatoria. Cuantificando los momentos, si existen, podemos tener medidas, tanto de posición como de dispersión o forma.

Momento de una variable aleatoria bidimensional:

Momento de una variable aleatoria unidimensional:

Esperanza matemática: Se denota por E(X) o µ, y se calcula de la siguiente forma Se define la esperanza matemática (o simplemente esperanza) de una variable aleatoria X como su valor medio.^