VM266 1418

Definition of the limit of a function:

Let a function f be defined on an open interval containing a, except possibly a itself, and let L be a real number. The statement

lim f(x) = L
x->a

means that for every ε > 0, there is a δ > 0 such that

if 0 < |x-a| < δ, then |f(x) - L| < ε

Alternative definition of limit:

lim f(x) = L
x->a

means that for every ε > 0, there is a δ > 0 such that if x is in the open interval (a - δ, a + δ) and x ≠ a, then f(x) is in the open interval (L - ε, L + ε).

Example:

Proove that lim (3x-5) = 7
x->4

let f(x) = 3x-5, a = 4, and L = 7.

if 0 < |x - 4| < δ, then |(3x-5) - 7| < ε

|(3x - 5) - 7| < ε
|3x - 12| < ε
|3(x - 4)| < ε
3|x - 4| < ε
|x - 4| < 1/3 ε

0 < |x-4| < δ
0 < |x-4| < 1/3ε
0 < 3|x-4| < ε
0 < |3x-12| < ε
0 < |(3x - 5) - 7| < ε

This verifies and completes the proof

Limits involving infinity:

lim f(x) = L
x->∞

means that for every ε > 0, there is a number M > 0 such that

if x > M, then |f(x) - L| < ε




lim f(x) = L
x->-∞

means that for every ε > 0, there is a number N < 0 such that

if x < N, then |f(x) - L| < ε




lim f(x) = ∞
x->a

means that for every M > 0, there is a δ > 0 such that

if 0 < |x - a| < δ, then f(x) > M

Techniques for finding limits:

I - lim [f(x) + g(x)] = lim f(x) + lim g(x)
x->a x->a x->a

II - lim [f(x) · g(x)] = lim f(x) · lim g(x)
x->a x->a x->a

III - lim [f(x)/g(x)] = lim f(x) / lim g(x)
x->a x->a x->a

IV - lim [c·f(x)] = c[lim f(x)]
x->a x->a

V - lim[f(x) - g(x)] = lim f(x) - lim g(x)
x->a x->a x->a

VI - lim [f(x)]^n = [lim f(x)]^n
x->a x->a

Sandwich/Squeeze Theorem:

Suppose f(x)≤h(x)≤g(x) for every xЄ of an open interval containing a, except possiblt at a.

If lim f(x) = L = lim g(x), then lim h(x) = L
x->a x->a x->a

Some special limits:

- lim (sin x)/x = 1
x->0

- lim (1 - cos x)/x = 0
x->0

- lim log x = ∞
x->∞

- lim log x = -∞
x->0+

- lim c/(x^k) = 0
x->±∞
for any pos rational number k

if lim g(x) = b and if f is continuous at b, then
x->c

lim f(g(x)) = f(b) = f(lim g(x))
x->c x->c



If g is continuous at c and if f is continuous at b = g(c), then

I - lim f(g(x)) = f(lim g(x)) = f(g(c))
x->c x->c

II - the composite function f o g is continuous at c

lim f(x) = L iff lim f(x) = L = lim f(x)
x->a x->a- x->a+

Intermediate Value Theorem:

if f is continuous on a closed interval [a,b] and if w is any number between f(a) and f(b), then there is at least one number c in [a,b] such that f(c) = w

Continuity:

A function is continuous at a number c iff:

I - f(c) is defined

II - lim f(x) exists
x->c

III - lim f(x) = f(c)
x->c



Let f be defined on [a,b]. f is continuous on [a,b] if it is continuous on (a,b) and if

lim f(x) = f(a) and lim f(x) = f(b)
x->a+ x->b-

Polynomials are continuous at every real number c

A rational function q = f/g is continuous at every number except the numbers c such that g(c) = 0

If f and g are continuous at c, then the following are also continuous at c:

I - the sum of f+g
II - the difference f-g
III - the product fg
IV - the quotient f/g, provided g(c)≠0

If a function f is continuous and has no zeros on an interval, then either f(x) > 0 or f(x) < 0 for every x in the interval

∫ sin x dx = -cos x + c

∫cos x dx= sin x + c

∫ tan x dx=- ln cos x + c

∫sec 2 x dx=tan x + c

∫csc 2 x dx=- cot x + c

∫sec x tan x dx=sec x + c

∫csc x cot x dx=- csc x + c

∫ 1 / x dx=ln x + c

∫e x dx=e x + c

∫ 1 / √ (1 - x 2 ) dx=sin -1 x + c

∫ 1 / ( 1 + x 2 ) dx=tan -1 x + c

∫1/ x √ (x 2 -1) dx=sec -1 x + c

∫ sec x dx=ln [ sec x + tan x]

∫ csc x dx=- l [ csc x + cot x ]

Definition of a one-to-one function:

A function f with domain D and range R is a one-to-one function if whenever:

- a ≠ b in D, then f(a) ≠ f(b) in R.

- f(a) = f(b) in R, then a = b in D

- for every y in R there exists a unique x in D such that f(x) = y

Every increasing function is 1-1 because:

if a < b, then f(a) < f(b)

if b < a, then f(b) < f(a)

thus a ≠ b, then f(a) ≠ f(b)

Similarly, every decreasing function is 1-1

The horizontal line test is one way to check 1-1 graphically

Definition of an inverse function:

Let f be a 1-1 function with domain D and range R. A function g with domain R and range D is the inverse function of f, provided the following condition is true for every x in D and every y in R:

y = f(x) iff x = g(y)

Verification of g as an inverse:

Let f be a 1-1 function with domain D and range R. If g is a function with domain R and range D, then g is the inverse function of f iff both of the following conditions are true:

I - g(f(x)) = x for every x in D

II - f(g(y)) = y for every y in R

Proof:

Assume g is an inverse function of f

by the definition of an inverse function:
y = f(x) iff x = g(y)
for every x in D, for every y in R

I - x = g(y) = g(f(x))
II - y = f(x) = f(g(y))

Conversely, assume conditions I & II hold

Assume g is an inverse function of f

suppose y = f(x) for all x in D

from I - g(y) = g(f(x)) = x

therefore: y = f(x), for all x in D => x=g(y) for all y in R

conversely: x = g(y) for all y in R

from II - f(x) = f(g(y)) = y

therefore: x=g(y) for all y in R => y=f(x) for all x in D

The domain must be restricted when functions are not 1-1 to get an inverse

A 1-1 function ha a unique inverse function

Proof:

assume g_1 and g_2 are inverse functions of f

by def. of inverse functions:

y=f(x) <=> x = g_1(y) for all x in D, for all y in R
y=f(x) <=> x = g_2(y) for all x in D, for all y in R

then g_1(y) = g_2(y) for all y in R

therefore: g_1 = g_2

Let g be an inverse of f. The domain of g is the range of f and the range of g is the domain of f.

If f is continuous and increasing on [a,b], then f has an inverse function f^-1 that is continuous and increasing on
[f(a), f(b)].

If a differentiable function f has an inverse function g = f^-1 and if f'(g(c)) ≠ 0, then g is differentiable at c and

g'(c) = 1/f'(g(c))

This can be restated as follows:

If g is the inverse function of a differentiable function f and is f'(g(x)) ≠ 0, then

g'(x) = 1/f'(g(x))

Proof:

By the definition of the derivative:

g'(c) = lim g(x) - g(c)
x->c x - c

Let y = g(x) and a = g(c). Since f and g are inverse functions of each other,

g(x) = y <=> f(y) = x
g(c) = a <=> f(a) = c

since f is differentiable, it is continuous and hence, so is the inverse function g = f^-1. Thus, if x->c then g(x) -> g(c); that is, y->a. If y->a, then f(y) -> f(a). Thus, we may write

g'(c) = lim g(x) - g(c)
x->c x - c

= lim y - a
y->a f(y) - f(a)

= lim 1
y->a f(y) - f(a)
y - a

= 1
lim f(y) - f(a)
y->a y - a

= 1 = 1
f'(a) f'(g(c))

Guidelines for finding f^-1 in simple cases:

1. Verify that f is a 1-1 function (or that it is increasing or decreasing) throughout its domain

2. Solve the equation y=f(x) for x in terms of y, obtaiing an equation of the form x = f^-1(y)

3. Verify the two conditions:

f^-1(f(x)) = x andf(f^-1(x)) = x

for every x in the domains of f anf f^-1, respectively.

Some Properties:

lim (1+h)^1/h = e
h->0

lim (1+1/n)^n = e
n->∞

x' = xcosꝊ + ysinꝊ
y' = -xsinꝊ + ycosꝊ
x = x'cosꝊ - y'sinꝊ
y = y'cosꝊ + x'sinꝊ

To eliminate xy term in Ax^2 + Bxy + Cy^2 + Dx + Ey + F :

pick Ꝋ such that cot2Ꝋ = (A-C)/B
0 < 2Ꝋ < pi

then use rotation of axes formulas above

Intermediate Value Theorem:

if f(x) is continuous on [a,b], then for every M between f(a) and f(b), there exists at least one value c in [a,b] such that f(c) = M

Mean Value Theorem:

If f(x) is continuous on [a,b] and differentiable on (a,b), then there exists a value c in (a,b) such that f'(c) = f(b) - f(a) / b-a

Extreme Values on a Closed Interval:

If f(x) is continuous on a closed interval [a,b], then f attains both a maximum and minimum value on [a,b]. Furthermore, if c in [a,b] and f(c) is an extreme value (min or max), then c is either a critical point or one of the endpoints, a or b.

The fundamental Theorem of calculus:

(i) Assume that f(x) is continuous on [a,b] and differentiable on (a,b). Let F(x) be an antiderivative of f(x) on [a,b]. Then

b
ʃ f(x) dx = F(b) - F(a)
a

(ii) Assume f(x) is continuous on [a,b] and differentiable on (a,b).
x
Then the area function A(x) = ʃ f(t) dt is an antiderivative of f
a

That is A'(x) = f(x) or:

x
d/dx ʃ f(t) dt = f(x)
a

Furthermore, A(x) satisfies the initial condition A(a) = 0.

Definition of the Derivative:

The slope m_a of the tangent line to the graph of the function f at P(a, f(a)) is

m_a = lim f(a+h) - f(a)
h->0 h

provided the limit exists.



The derivative of a function f is the function f′ defined by

f′(x) = lim f(a+h) - f(a)
h->0 h

provided the limit exists.

Because of the above two definitions, f′(x) = m_a

Alternate definition of the derivative:

f′(a) = lim f(x) - f(a)
x->a x - a

Determining differentiability:

A function f is differentiable on a closed interval [a,b] if f is differentiable on the open interval (a,b) and if the following limits exist:

lim f(a+h) - f(a) and lim f(b+h) - f(b)
h->0+ h h->0- h

If a function is differentiable at a, then f is continuous at a

Vertical tangent lines:

The graph of a function f has a vertical tangent line x = a at the point P(a, f(a)) if f is continuous at at and if

lim |f'(x)| = ∞
x->a


A point P(a,f(a)) on the graph of a function f is a cusp if f is continuous at a and if the following two conditions hold:

I - f'(x) -> ∞ as x approaches a from one side
II - f'(x) -> -∞ as x approaches a from the other side

Techniques of differentiation:

- let n be an integer
- let c be a contstant

Note: proofs can be done by using the definition of the derivative

Power Rule:
if f(x) = cx^n, then f'(x) = cnx^(n-1)

I - Dx c = 0
II - Dx (mx + b) = m
III - Dx (x^n) = nx^(n-1)
IV - Dx [cf(x)] = c Dx f(x)
V - Dx [f(x) + g(x)] = Dx f(x) + Dx g(x)
VI - Dx [f(x) - g(x)] = Dx f(x) - Dx g(x)
VII - Dx f(x)g(x) = g(x)Dx f(x) + f(x)Dx g(x)
VIII - Dx [f(x)/g(x)] = g(x)Dx f(x) - f(x)Dx g(x)
[g(x)]^2
IX - Dx[1/g(x)] = -Dx g(x)
[g(x)]^2

Some notable derivatives:

- Dx sin x = cos x
- Dx cos x = -sin x
- Dx tan x = sec^2 x
- Dx cot x = -csc^2 x
- Dx sec x = sec x tan x
- Dx csc x = -csc x cot x

Notation:

f'(x) = D_x f(x) = D_x y = y' = dy/dx = d/dx f(x)

Hihger derivatives:

f''(x), f'''(x), f(⁴)(x),....,f^(n)(x)
D_x y, D²_x y,...,(D_x)^n y
d²y/dx², d³y/dx³,...,d^n y/dx^n

Below is a list of how characters are used in this map:

_ after a variable indicates a subscript. i.e. x_1 means x subscript 1

^ indicates raising to a power. i.e. x^2 means x squared

Definite integrals are denoted ∫(a->b) x dx where a is the bottom number of the integral and b is the top

Definition:

ln x = ∫(1->x) 1/t dt if x≥1

-lx x = ∫(x->1) 1/t dt if 0<x<1

Laws of ln:

I - ln pq = ln p + ln q
II - ln p/q = ln p - ln q
III - ln p^r = r ln p for all rational r

Definitions of Hyperbolic Functions:

sinh x = e^x - e^-x
2

cosh x = e^x + e^-x
2

tanh x = e^x - e^-x
e^x + e^-x

coth x = e^x + e^-x
e^x - e^-x

sech x = 2
e^x + e^-x

csch x = 2
e^x - e^-x

Some properties:

cosh^2 x - sinh^2 x = 1

1 - tanh^2 x = sech^2 x

coth^2 x - 1 = csch^2 x

e^iθ = cosθ + i sinθ = cisθ

e^-iθ = cosθ - i sinθ = cisθ

cosh iθ = cosθ

sinh iθ = i sinθ

cos it = cosh t

cosh^2 t + sinh^2 t = cosh 2t

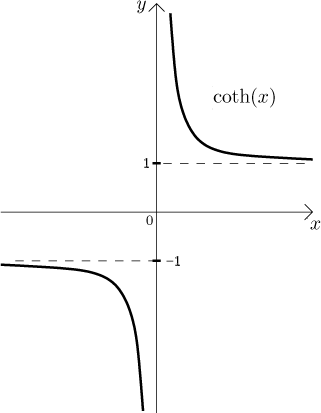
Derivatives:

- Dx sinh u = cosh u Dx u
- Dx cosh u = sinh u Dx u
- Dx tanh u = sech^2 u Dx u
- Dx coth u = -csch^2 u Dx u
- Dx sech u = -sech u tanh u Dx u
- Dx csch u = -csch u coth u Dx u

Integrals:

∫sinh u du = cosh u + C
∫cosh u du = sinh u + C
∫sech^2 u du = tanh u + C
∫csch^2 u du = -coth u + C
∫sech u tanh u du = -sech u + C
∫csch u coth u du = -csch u + C

A sequence is a function f whose domain is the set of positive integers.

A sequence {a_n} has the limit L, or converges to L, if for every E>0 there exists a positive number N such that |a_n - L| < E whenever n>N

We say that limit = L

if we can make an as close to L as we want for all sufficiently large n. In other words, the value of the an’s approach L as n approaches infinity.

We say that limit = infinity



if we can make an as large as we want for all sufficiently large n. Again, in other words, the value of the an’s get larger and larger without bound as n approaches infinity.

We say that limit = negative infinity



if we can make an as large and negative as we want for all sufficiently large n. Again, in other words, the value of the an’s are negative and get larger and larger without bound as n approaches infinity.

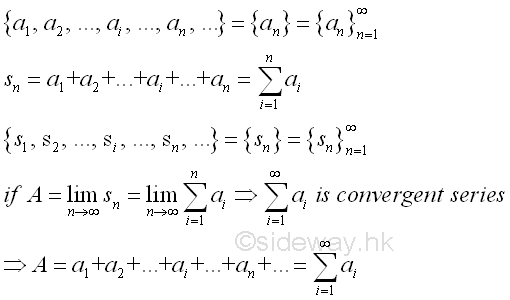
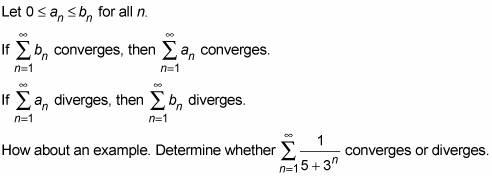
Convergence and divergence tests

Divergence test

If limn→∞an does not exist or if limn→∞an ≠ 0, then the series ∑an is divergent.

Integral test

(a) If ∫ƒ(x)dx is convergent, then ∑an is convergent.

(b) If ∫ƒ(x)dx is divergent, then ∑an is divergent.

p-series

The p-series ∑1/np is convergent if p>1 and divergent if p≤1.

Limit comparison

If limn→∞an/bn=c where 0<c<∞, then either both series converge or both series diverge.

Alternating Series test

(i) bn+1≤bn for all n

(ii) limn→∞bn=0

then the series is convergent.

Test for Absolute Convergence

If the ∑|an| converges, then the ∑an absolutely converges.

Ratio Test

limn→∞|an+1/an|=L:

(i) If L<1, then the series ∑an is absolutely convergent.

(ii) If L>1 or L=∞, then the series ∑an is divergent.

(iii) If L=1, inconclusive.

Root test

IF lim n->oo (An)^1/n = L, L < 1 Series An is abs. convergent. L > 1 || L = oo series is divergent. L = 1 inconclusive.

Geometric series

ar^n-1

convergent if |r|<1, sum = a/1-r
divergent if |r|>=1

Power Series

Theorem: For a power series ∑ck(x-x0)k, exactly one of the fallowing statements is true

a) The series converges only for x=x0

b) The series converges absolutely for all real values of x

c) Th series converges absolutely for all x in some finite open interval is (x0-R,x0+R) and diverges if x<x0-R or x>x0+R. At either of the values x=x0-R or x=x0+R, the series may converge absolutely, converge conditionally, or diverge, depending on the particular series.

Theorem: For any power series in x, exactly one of the following is true:

a) the series converges for x=o

b) the series converges absolutely for all real values of x

c) the series converges absolutely for all x in some finite open interval (-R,R) and diverges if x<-R or x>R. At either of the values x=R or x=-R, the series may converge absolutely, converge conditionally, or diverge depending on the particular series.

r = a is a circle
Ꝋ = a is a line
r = +- asinꝊ is a circle above/below the origin
r = +- acosꝊ is a circle right/left of the origin
r = a(1+-cosꝊ) is a cardioid right/left of the origin
r = a(1+-sinꝊ) is a cardiod above/below the origin
r = a+-bsinꝊ is a limacon right/left of origin
r = a+-bcosꝊ is a limacon above/below origin

r = asin nꝊ or r = acos nꝊ has 2n loops if n is even, n loops if n is odd

r = aꝊ is a spiral

x = rcosꝊ
y = rsinꝊ
r^2 = x^2 + y^2
tanꝊ = y/x if x not 0

slope m = dy/dx = (dy/dꝊ) / (dx/dꝊ)
= (dr/dꝊ * sinꝊ + rcosꝊ) / (dr/dꝊ * cosꝊ - rsinꝊ)

Integrals:

Area A = ʃ1/2 r^2 dꝊ

Arclength L = ʃ [r^2 + (dr/dꝊ)^2]^1/2 dꝊ
ds = [r^2 + (dr/dꝊ)^2]^1/2 dꝊ

Surface of Revolution about x axis S = ʃ2pi y ds
= ʃ2pi rsinꝊ [r^2 + (dr/dꝊ)^2]^1/2 dꝊ
About y axis S = ʃ2pi x ds
= ʃ2pi rcosꝊ [r^2 + (dr/dꝊ)^2]^1/2 dꝊ

Polar Conics:

r = de/1+-ecosꝊ ; r = de/1+-esinꝊ

e = 1 => parabola
e > 1 => hyperbola
0 < e < 1 => ellipse and e=c/a

Parametric Surface Area: x = f(t); y = g(t)

S = ʃ 2pi y ds = ʃ2pi g(t)[f'(t)^2 + g'(t)^2]^1/2 dt

About Y axis:

S = ʃ 2pi x ds = ʃ2pi f(t)[f'(t)^2 + g'(t)^2]^1/2 dt

Arc Length:

L = ʃ [f'(t)^2 + g'(t)^2]^1/2 dt
ds = [f'(t)^2 + g'(t)^2]^1/2 dt

Derivative:

dy/dx = (dy/dt) / (dx/dt) if dx/dt not zero

d^2 y/ dx^2 = (dy'/dt) / (dx/dt)