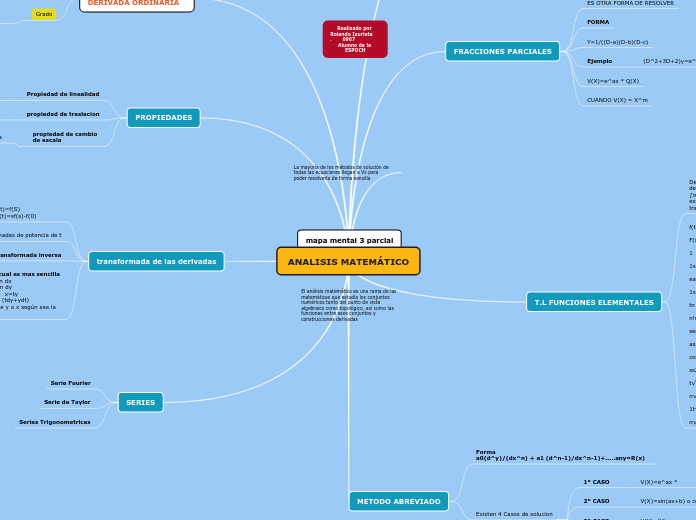
ANALISIS MATEMÁTICO

Più simili a questo

R A D I C A L E S

da Michelle Carce

cartilla clasificación documental

da mayra guerrero

Piña

da Vanne Ruiz

CSS

da Maria Paula Garcia Forero

mapa mental 3 parcial

Realizado por Rolando Izurieta . 6967 Alumno de la ESPOCH

El análisis matemático es una rama de las matemáticas que estudia los conjuntos numéricos tanto del punto de vista algebraico como topológico, así como las funciones entre esos conjuntos y construcciones derivadas

ANALISIS MATEMÁTICO

SERIES

Series Trigonometricas

Serie de Taylor

Serie Fourier

transformada de las derivadas

Veo entre N y M cual es mas sencilla N esta asociada con dx M esta asociada con dy y=tx o x=ty (tdx+xdt) (tdy+ydt) remplazo la variable y o x según sea la mas adecuada

Transformada inversa

f(s) = F(t)

Transformadas de potencia de t

si L < F(t)

F(t)= e^2t*(t+1)*sin 3t

SI L{f(t)=f(S) =L { F(t)=sf(s)-f(0)

La mayoría de los métodos de solución de todas las ecuaciones llegan a Vs para poder resolverla de forma sencilla

PROPIEDADES

propiedad de cambio de escala

SI L { F(T) = f(s) y G(t) {F(t-a) t >a,,, 0 t

propiedad de traslacion

SI L { F(t) = f(s)

Propiedad de linealidad

SI L{C1f1(t)+C2F2(t)=C1 L{F1(T)+C2 L {F2(T)

TIPOS DE ECUACIONES DERIVADA ORDINARIA

Grado

Exponente del mayor orden en EDO

Orden

Mayor orden de la derivada presente en EDO

METODO ABREVIADO

Existen 4 Casos de solucion

4º CASO

V(X)=e^ax*Q(X)

y=1/F(D) * V(X)

3º CASO

V(X)=X^m

y=1/F(D) * X^m

2º CASO

V(X)=sin(ax+b) o cos(ax+b)

F(D)y=V(X)

1º CASO

V(X)=e^ax *

(D^2-3D+2)Y=e^x

Forma a0(d^y)/(dx^n) + a1 (d^n-1)/dx^n-1)+.....any=R(x)

T.L FUNCIONES ELEMENTALES

f(t) (t>0) F(s)=L[f] 1 1s , s>0 eat 1s−a , s>a tn , n natural n!sn+1 , s>0 senat as2+a2 , s>0 cosat ss2+a2 , s>0 t√ π√2s−3/2 , s>0 1t√ π√s−1/2 , s>0

Definición(Transformada de Laplace).- Sea f(t) una función definida en t≥0. Si la integral ∫∞0e−stf(t)dt existe para algunos valores de s, se dice que es la transformada de Laplace de f(t).

FRACCIONES PARCIALES

CUANDO V(X) = X^m

V(X)=e^ax * Q(X)

Ejemplo

(D^2+3D+2)y=e^x

Y=1/((D-a)(D-b)(D-c)

FORMA

ES OTRA FORMA DE RESOLVER

METODODEINTEGRALES SUCECIVAS

Yg = P(D)=? P/(D)*Y= V(X) Y=1/P(D)*V(X) Y= 1/((D-a)(D-a2)....(D-an) * V(X)

Cuando tenemos el producto de un polinomio por una función del tipo sen x , cos x , ax al derivar el polinomio se simplifica, y al integrar las demás funciones no se complica