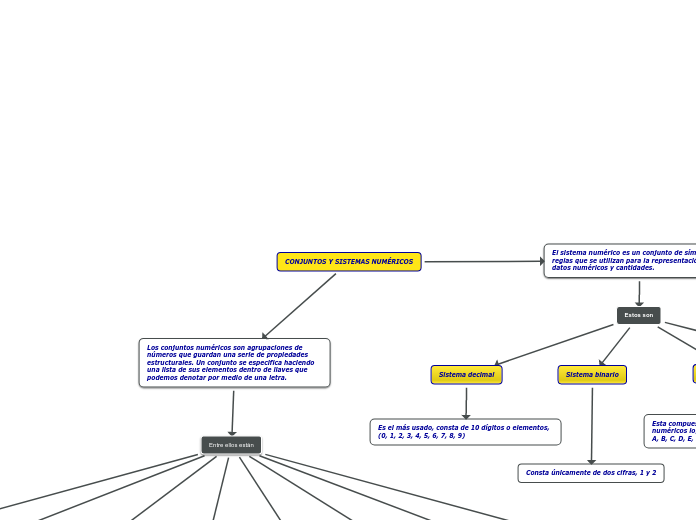
CONJUNTOS Y SISTEMAS NUMÉRICOS

Più simili a questo

TEORIA DE LAS RELACIONES HUMANAS

da ana villa

La historia del numero 1

da Joaquín Felix

INTRODUCCION AL PENSAMIENTO COMPLEJO

da Gabby del Pilar Dávila Penen

TIPOS DE NUMEROS

da Gerardo Bayas

CONJUNTOS Y SISTEMAS NUMÉRICOS

El sistema numérico es un conjunto de símbolos y reglas que se utilizan para la representación de datos numéricos y cantidades.

Estos son

Sistema octal

Esta compuesto por 8 números 0, 1, 2, 3, 4, 5, 6, 7.

Sistema Hexadecimal

Esta compuesto por un grupo de signos alfa numéricos los cuales son 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.

Sistema binario

Consta únicamente de dos cifras, 1 y 2

Sistema decimal

Es el más usado, consta de 10 dígitos o elementos, (0, 1, 2, 3, 4, 5, 6, 7, 8, 9)

Los conjuntos numéricos son agrupaciones de números que guardan una serie de propiedades estructurales. Un conjunto se especifica haciendo una lista de sus elementos dentro de llaves que podemos denotar por medio de una letra.

Entre ellos están

Números complejos

Elemento del conjunto numérico surgido para resolver ecuaciones algebraicas que involucren raíz cuadrada de un número negativo, se denota con la letra C.

Números imaginarios

Son números complejos cuya parte real es igual a 0, se denota con la letra i.

i= raíz cuadrada de -1 -i. 5i. 2,5i. -8i.

Números reales

Son el conjunto que incluye los números naturales, enteros, racionales e irracionales, se denota con la letra N.

Son ejemplos de números reales los siguientes: e, π (pi), √2, -√2, √3, -√5, 1/3, -2/5, 8/7, 1, -4, 0, 5...

Números irracionales

Es un número que no se puede escribir en fracción, el decimal sigue para siempre sin repetirse, se denota con la letra I.

π (pi): Se trata de la expresión de la relación que existe entre el diámetro de una esfera y su longitud. Pi entonces es 3.141592653589 (…), aunque en general se lo conoce simplemente como 3.14. √5: 2.2360679775 √123: 11.0905365

Números racionales

Aquellos números que pueden representarse como el cociente de dos enteros, con denominador distinto a cero, se denota con la letra Q.

69,96 (1749/25) 7,2 (36/5) 3,333333 (3/10) 86,5 (173/2)

Números fraccionarios

Son la expresión de una cantidad dividida en otra cantidad, se denota con la letra Q*.

4/5, 21/13, 61/2, 1/3

Números enteros

Es un elemento del conjunto numérico que contiene los números naturales, a sus inversos negativos y el cero, se denota con la letra Z.

...-2, -1, 0, 1, 2...

Números naturales

Son los números que se usan para contar los elementos de un conjunto, se denota con la letra N.

N = {1, 2, 3, 4, 5, 6...}