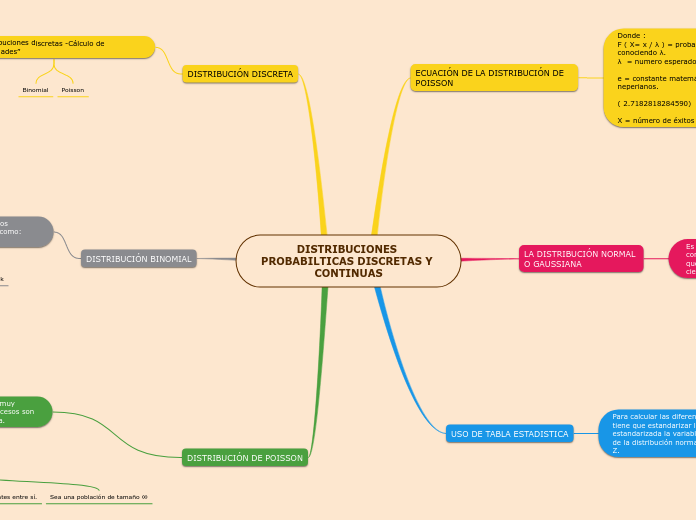
DISTRIBUCIONES PROBABILTICAS DISCRETAS Y CONTINUAS

Più simili a questo

Teoria de la demanda, Teoria de la oferta y Precio de equilibrio

da Carlos Jimenez

ECUACIÓN CUADRÁTICA

da Dennise Maricela Zambrano Meza

Organigrama arbol

da Andrea Puga

FIGURAS CÓNICAS

da Brenda Silvana Toro Castillo

DISTRIBUCIONES PROBABILTICAS DISCRETAS Y CONTINUAS

USO DE TABLA ESTADISTICA

Para calcular las diferentes probabilidades se tiene que estandarizar la variable. Una vez estandarizada la variable, recién utilizar la tabla de la distribución normal estandarizada o tabla Z.

LA DISTRIBUCIÓN NORMAL O GAUSSIANA

Es importante porque las variables aleatorias continuas (peso, edad, talla, etc ) son variables que más se evalúan en una investigación científica

ECUACIÓN DE LA DISTRIBUCIÓN DE POISSON

Donde : F ( X= x / λ ) = probabilidad de que X = x conociendo λ. λ = numero esperado de éxitos. e = constante matemática base de los logaritmos neperianos. ( 2.7182818284590) X = número de éxitos por unidad.

DISTRIBUCIÓN DE POISSON

Esta distribución de probabilidades es muy utilizada para situaciones donde los sucesos son impredecibles o de ocurrencia aleatoria.

Se caracteriza por:

Sea una población de tamaño ∞

Los sucesos son independientes entre sí.

Sea una muestra de tamaño n bastante elevado

DISTRIBUCIÓN BINOMIAL

Distribución experimental que tenga dos respuestas, generalmente se clasifica como: éxito y fracaso

f(k) = P [ X= k] = nCk . pk . qn-k

DISTRIBUCIÓN DISCRETA

Las distribuciones discretas -Cálculo de probabilidades”

Poisson

Binomial