da John Rodgers mancano 3 anni
335
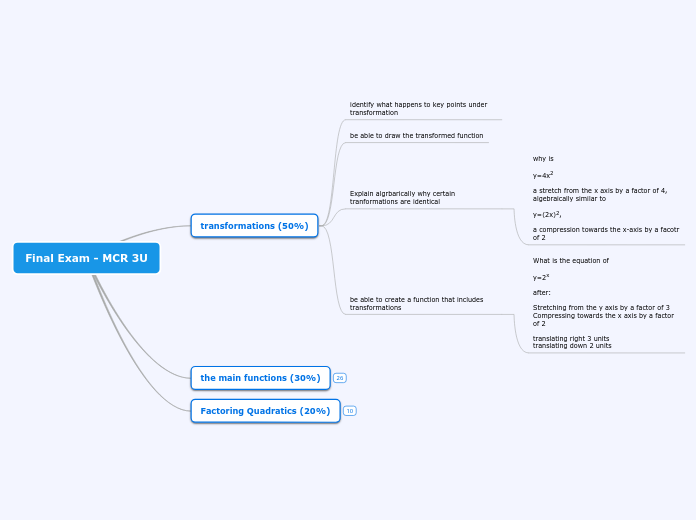
Final Exam - MCR 3U
da John Rodgers mancano 3 anni
335

Più simili a questo
The quadratic formula
be able to use the discriminant
a tricky trinomial
0=4x2+4x+1
simpe trinomial
0=x2+5x+6
a differnce of squares
0=16x2-25
y=2(x+3)+4
y=3sin(2(x+60))+5
y=(x-2)2+3
be able to state the ratios for the special angles
istem speed test
be able to model with trig functions
be able to create a function with a prescribed amplitude, period, phase shoft and vertical displacement
be able to solve using various techniques
be able to work with 1/2 lives
coleum, a medical isotope used to control evil legs, has a 1/2 life of 12 hours. Create a function to model the amount of coleum at time t, A(t), given the initial amount Ao
coleum a medical isotope has a 1/2 life of 12 hours. What percentage is left after 4 days?