da Nur Maisarah Hashim mancano 9 anni
704
How To Prove Conditional Statement
da Nur Maisarah Hashim mancano 9 anni
704

Più simili a questo
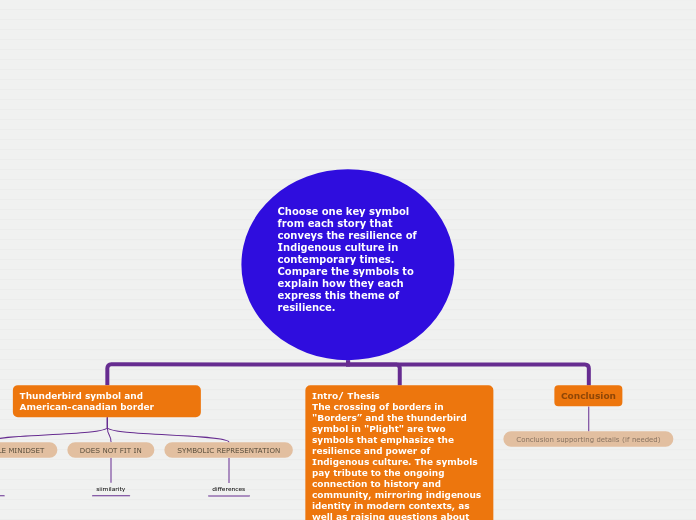

da Sasha Lang

da Art Scrivener

da Shu Braque


da Natalia Martinez Garzon
Proposition if P, then Q. Proof. Suppose ~ Q . . . Therefore ~ P
If X is odd, then X^2 is
Proposition P. Proof. Suppose ~ P . . . Therefore C^ ~C
Prove that if n is an integer and 3n+2 is even, then n is even using a contradiction
For the sake of contradiction, Suppose 3n+2 is even, and n is odd n = 2a+1 3n+2 = 3 (2a+1) + 2 = 6a+3+2 = 6a+5 = 2 (3a+2) + 1 = 2b+1 , b = 3a +2, a ∈ Z From the last line, 3n+2 is odd but previously we deduced that 3n+2 is even. It is contradiction. Therefore, the given preposition is true.
Example :
If X is odd, then X^2 is odd.
Suppose X is odd. Then, X = 2a + 1 Thus, X^2 = ( 2a + 1 ) ^2 = 4a^2 + 4a + 1 = 2 ( 2a^2 + 2a) + 1 = 2b + 1 , b = 2a^2 + 2a, a ∈ Z