da MONTANO DE ANGEL ISABELLA mancano 2 anni
216
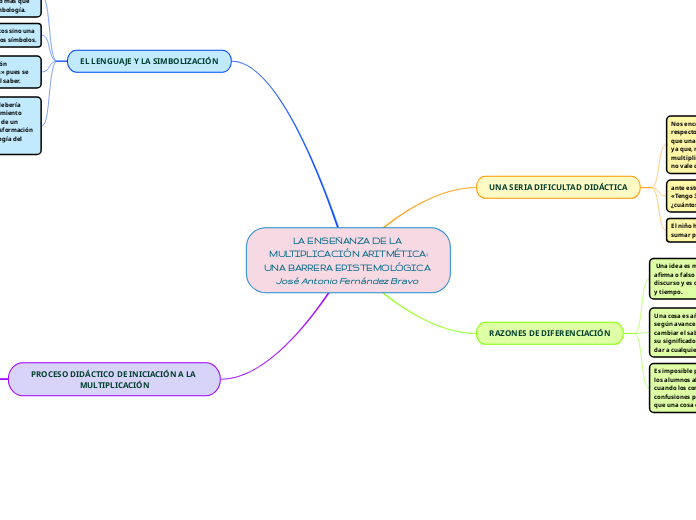
LA ENSEÑANZA DE LA MULTIPLICACIÓN ARITMÉTICA: UNA BARRERA EPISTEMOLÓGICA José Antonio Fernández Bravo
da MONTANO DE ANGEL ISABELLA mancano 2 anni
216

Più simili a questo