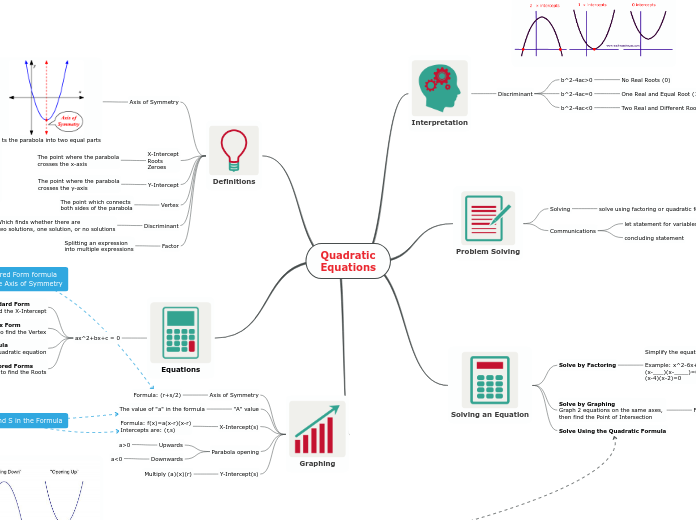
Quadratic Equations

Più simili a questo

Quadratics Concept Map Assignment

da Rushikesh Amin

Vertex Form

da DANIEL SHANG

MATH 1512-70

da Jackie Lindquist

I am learning different ways to describe objects.

da Andrea Fischer

Quadratic Equations

Graphing

Y-Intercept(s)

Multiply (a)(x)(r)

Parabola opening

Downwards

a<0

Upwards

a>0

X-Intercept(s)

Formula: f(x)=a(x-r)(x-r) Intercepts are: (r,s)

"A" value

The value of "a" in the formula

Formula: (r+s/2)

Equations

ax^2+bx+c = 0

Factored Forms Used to find the Roots

f(x) = a(x-r )(x-r )

Quadratic Formula Used to solve a quadratic equation

(-b±√b^2-4ac) / 2a

Vertex Form Used to find the Vertex

Vertex y = a(x – h)^2 + k

Standard Form To find the X-Intercept

y=ax^2+bx+c

Definitions

Factor

Splitting an expression into multiple expressions

Which finds whether there are two solutions, one solution, or no solutions

Vertex

The point which connects both sides of the parabola

Y-Intercept

The point where the parabola crosses the y-axis

X-Intercept Roots Zeroes

The point where the parabola crosses the x-axis

Axis of Symmetry

splits the parabola into two equal parts

Solving an Equation

Solve Using the Quadratic Formula

Solve by Graphing Graph 2 equations on the same axes, then find the Point of Intersection

Finding the Point of Intersection

1) solve for x 2) plug the value of x into the original equation to find y

Solve by Factoring

Simplify the equation Example: x^2-6x+8=0 (x-___)(x-____)=0 (x-4)(x-2)=0

Zero Product Property When equation has product of two simple equations, one of the two (or both) must be equal to zero

1) Factor 2) Find the 2 Solutions 3) Solve each Equation

Example: (x-4)(x-2) (x-4)=0 because x=4 and/or (x-2)=0 because x=2

Problem Solving

Communications

concluding statement

let statement for variables

Solving

solve using factoring or quadratic formula

Interpretation

Discriminant

b^2-4ac<0

Two Real and Different Roots (3)

b^2-4ac=0

One Real and Equal Root (1)

b^2-4ac>0

No Real Roots (0)