da Francesco Basile mancano 5 anni
781
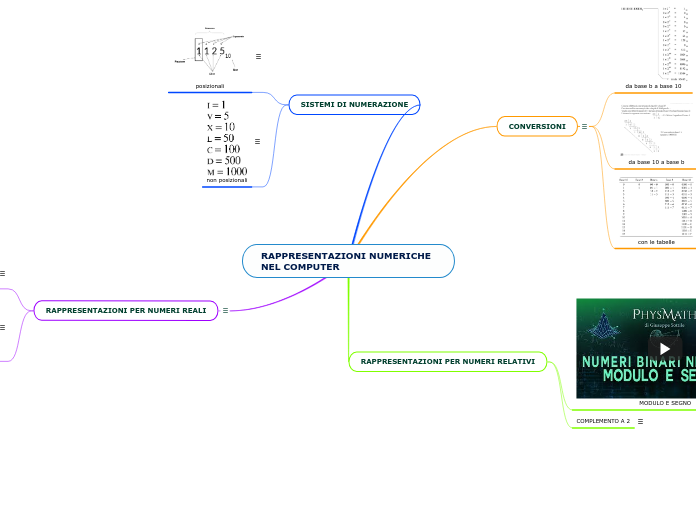
RAPPRESENTAZIONI NUMERICHE NEL COMPUTER
da Francesco Basile mancano 5 anni
781

Più simili a questo
Le due rappresentazioni possibili per i numeri reali sono in VIRGOLA FISSA(fixed point) e in VIRGOLA MOBILE(floating point).
Passiamo invece alla conversione in virgola mobile che si serve di 32 bit.
Partiamo dal numero +43,6875. Come sempre facciamo la conversione della parte intera, ottenendo 101011, e della parte decimale:
0,6875x
2
1,3750 Anche in questo le cifre intere vanno poi usate nella rappresentazione finale.
2
0,750
2
1,500
2
3,000
Mettendo quindi insieme la parte intera e quella decimale, otteniamo 101011,1011.
A questo punto dobbiamo NORMALIZZARE, cioè portare la virgola fino alla prima cifra a sinistra, quindi 1,010111011x2⁵(alla quinta perchè abbiamo spostato la virgola di 5 posizioni).
Le cifre dopo la virgola fanno parte della MANTISSA. Ora dobbiamo POLARIZZARE: il 5 viene sommato a 127(BIAS),ottenendo 132. Questo numero viene convertito in binario, ottenendo 10000100, che forma l’ESPONENTE.
Possiamo quindi procedere a rappresentare in virgola mobile:
010000100010111011000000000000000
con lo 0 in blu che indica il segno, la parte in verde che indica l’esponente, la parte in giallo che indica la prima parte della mantissa e i restanti 0 in rosso che completano la mantissa.
La rappresentazione in virgola fissa richiede un formato di 16 bit: 1 per il segno, 7 per la parte intera e 8 per la parte decimale. Partendo dal numero -36,625, svolgiamo la conversione in binario della parte intera, ottenendo (100100) e in seguito, utilizzando il metodo delle moltiplicazioni successive, moltiplichiamo la parte decimale fino a trovare un numero intero:
0,625x
2 = Le cifre in rosso vengono tolte dalla moltiplicazione e messe nella rappresentazione finale
1,250
2
0,500
2
1,000
La rappresentazione finale è quindi:
1010010010100000
Con il primo 1 che indica il segno, le successive 7 cifre la parte intera(lo 0 in rosso per completare i 7 bit) e le altre 8 per la parte decimale(gli ultimi 5 zeri in rosso per completare gli 8 bit).
Il sistema non posizionale principale è quello dei numeri romani.
I sistemi posizionali sono: il sistema decimale, ottale, binario, esadecimale,ecc.
La rappresentazione in complemento a 2, invece, rimane invariata se dobbiamo convertire un numero positivo, quindi rimarrebbe la stessa usando il MS, mentre se bisogna rappresentare un numero negativo il discorso diventa un po’ più articolato; prendiamo ad esempio -102, facciamo la conversione in binario e troviamo (1100110). Adesso la conversione in MS del numero positivo sarebbe 01100110: queste cifre vanno adesso invertite, trovando il numero in complemento a uno, quindi 10011001. Questo numero va adesso sommato a 1, trovando quindi 10011010. La trasformazione in complemento a due è completata.
La rappresentazione in modulo e segno si svolge partendo dalla conversione: in questo caso -90 diventa (1011010) in binario.
Essendo però un numero negativo e dovendo raggiungere 8 bit, la rappresentazione finale in modulo e segno di -90 diventa: 11011010. La cifra in rosso rappresenta il meno, infatti questo segno viene rappresentato appunto con l’1, mentre il + con lo 0.
Nella conversione, il processo che ci permette di convertire un numero in un’altra base qualsiasi, l’ultima cifra da destra equivale alle unità, la seconda alle decine e così via.
Per convertire un numero in base 2 in uno in base 8 o 16 utilizzeremmo delle conversioni indirette, cioè passare dalla base 2 alla base 10 per poi arrivare alle base 8 o 16. C’è però un metodo più veloce, utilizzare le conversioni con le tabelle. Questo metodo si serve di due tabelle, quella per la base 8 e quella per la base 16:
La tabella per la base 8 si costruisce scrivendo le cifre da 0 a 7 in verticale e, partendo dall’ultima colonna a destra, alternare l’1 allo 0, raddoppiando le cifre andando verso la colonna sinistra.
La tabella per la base 16, invece, si costruisce scrivendo le cifre da 0 a 9 e le lettere da A a F in verticale, e usando poi lo stesso procedimento usato per la tabella precedente.
Esempio di conversione in base 8:
(100110)₂=(46)₈
perchè 110=6
e 100=4.
Esempio di conversione in base 16:
(1101110110)₂=(376)₁₆
perchè 0110=6,
0111=7
e 0011=3. (le cifre in rosso sono aggiunte in modo da poter fare la conversione, quindi arrivare a 4 cifre).
Abbiamo quindi preso tre cifre partendo da sinistra per la base 8 e quattro per la base 16.
Per convertire invece, da base 10 a base 2, si utilizza il metodo delle divisioni successive:
(137)₁₀= (10001001)₂
Per scrivere il risultato, si inizia a leggere da sotto e si scrivono le cifre da sinistra a destra.
Per svolgere una conversione da base 2 a base 10 si usa la forma polinomia, cioè la sommatoria di ciascuna cifra moltiplicata per la base elevata alla sua posizione.
Ad esempio:
(1011)₂=1x2º+1x2¹+0x2²+1x2³=(11)₁₀