Измерение количества информации

Системы счисления

Систе́ма счисле́ния — символический метод записи чисел, представление чисел с помощью письменных знаков.

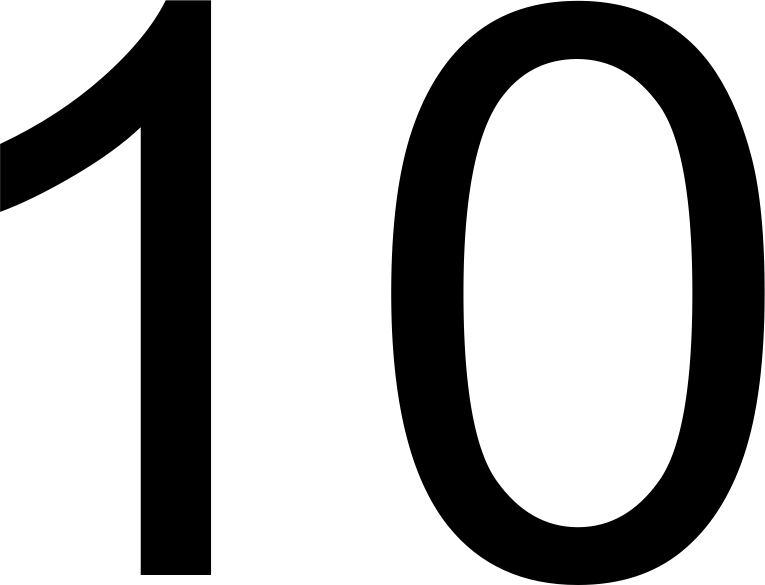
Десяти-ричная

Позиционная система счисления по основанию 10. Одна из самых распространенных систем счисления. Пример: число 103 записывается в десятичной системе счисления следующим образом: 103 = 1 * 10^2 + 0 * 10^1 + 3 * 10^0

Восьмеричная

Позиционная система счисления по основанию 8. Для представления чисел в ней используются цифры от 0 до 7. Восьмеричное число 15436 в десятичной записи будет выглядеть следующим образом: 1 * 8^4 + 5 * 8^3 + 4 * 8^2 + 3 * 8^1 + 6 * 8^0 = 6942

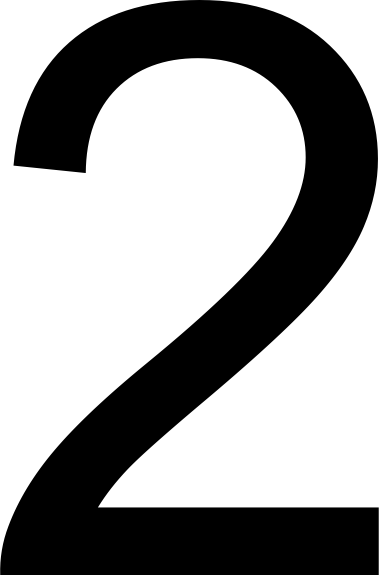
Двоичная

Двоичной системой счисления называется позиционная система счисления с основанием 2. Для записи чисел в ней использовали только две цифры: 0 и 1. Двоичное число 101 в десятичной записи будет иметь вид: 1 * 2^2 + 0 * 2^1 + 1 * 2^0 = 5

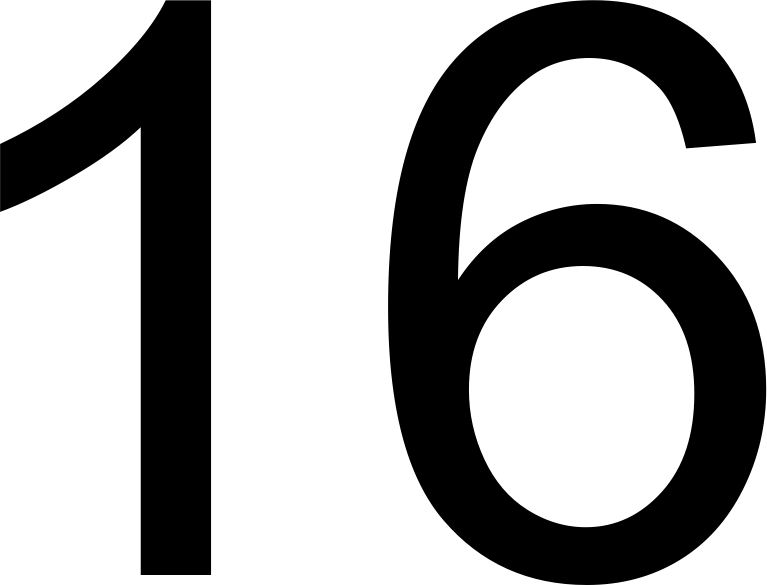
Шестнадцатиричная

Шестнадцатеричной системой счисления называется позиционная система счисления с основанием 16. Для записи чисел в шестнадцатеричной системе счисления используются цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 и латинские буквы A, B, C, D, E, F. Шестнадцатиричное число 2А7 в десятичной записи имеет вид: 2 * 16^2 + 10 * 16^1 + 7 * 16^0 = 512 + 160 + 7 = 679.

Вероятностный подход к измерению информации

Количество информации в сообщении о некотором событии зависит от его вероятности. Чем меньше вероятность события, тем больше информации оно несёт. Данный подход к измерению информации был разработан американским ученым Клодом Шенноном.

Pi – вероятность i-го события

N – количество возможных событий

I - информационный объем сообщения

Содержательный подход к измерению информации

В содержательном подходе количество информации, заключенное в сообщении, определяется объемом знаний, который это сообщение несет получающему его человеку.

Сообщение, уменьшающее неопределенность знания в два раза, несет 1 бит информации.

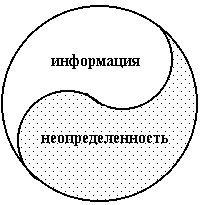
Неопределенность знания о результате некоторого события (бросание монеты или игрального кубика, вытаскивание жребия и др.) - это количество возможных результатов.

Сообщение об одном из двух равновероятных результатов некоторого события несет 1 бит информации.

Единицы измерения информации

Бит

Наименьшая единица измерения информации

Байт

1 байт = 8 бит

Килобайт

1 Килобайт = 1024 байт

Мегабайт

1 Мегабайт = 1024 Килобайт

Гигабайт

1 Гигабайт = 1024 Мегабайт

Терабайт

1 Терабайт = 1024 Гигабайт

Петабайт

1 Петабайт = 1024 Терабайт

Алфавитный подход к измерению информации

Алфавитный (объёмный) подход к измерению информации позволяет определить количество информации, заключенной в тексте, записанном с помощью некоторого алфавита.

Алфавит - множество используемых символов в языке (буквы, цифры, знаки препинания и пробел)

Формула Хартли

I - информационный вес символа

N - мощность алфавита - количество символов, используемых в алфавите.