Chapter 3
Polynomial Fucntion
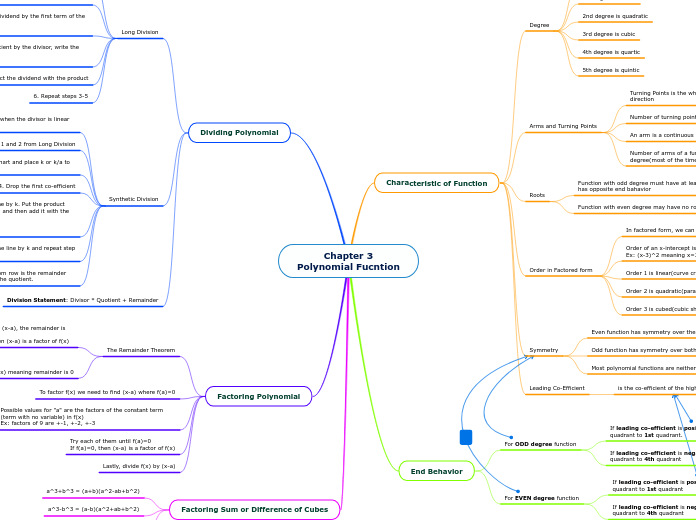
Characteristic of Function
Degree
is the exponent of the highest power
1st degree is linear
2nd degree is quadratic
3rd degree is cubic
4th degree is quartic
5th degree is quintic
Arms and Turning Points
Turning Points is the where the function change vertical direction
Number of turning points of a function is at most degree-1
An arm is a continuous lines in between 2 turning points
Number of arms of a function is determined by its degree(most of the time)
Roots
Function with odd degree must have at least 1 root because it has opposite end bahavior
Function with even degree may have no roots
Order in Factored form
In factored form, we can find x-intercept
Order of an x-intercept is its exponent
Ex: (x-3)^2 meaning x=3 has the order of 2
Order 1 is linear(curve crosses through x-axis)
Order 2 is quadratic(parabolic)
Order 3 is cubed(cubic shape)
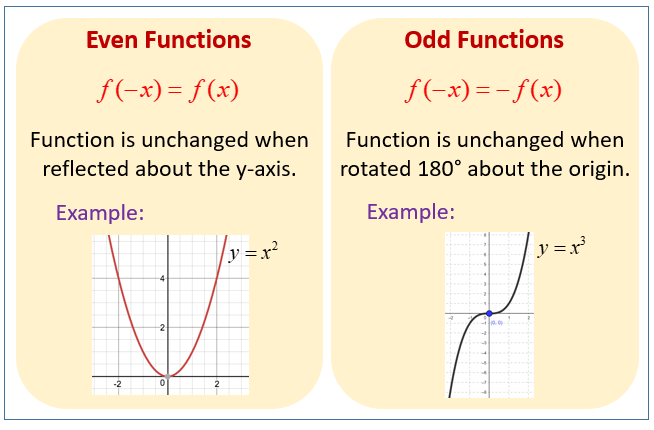
Symmetry
Even function has symmetry over the y-axis
Odd function has symmetry over both the x and y-axis
Most polynomial functions are neither
Leading Co-Efficient
is the co-efficient of the highest power
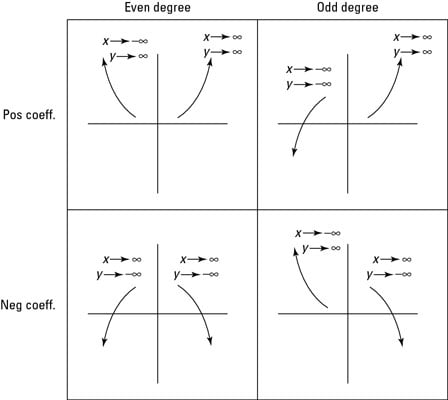
End Behavior
For ODD degree function
If leading co-efficient is positive, graph extends from 3rd quadrant to 1st quadrant.
x → -∞, y → -∞
x → +∞, y → +∞
If leading co-efficient is negative, graph extends from 2nd quadrant to 4th quadrant
x → -∞, y → +∞
x → +∞, y → -∞
For EVEN degree function
If leading co-efficient is positive, graph extends from 2nd quadrant to 1st quadrant
x → +-∞, y → ∞
If leading co-efficient is negative, graph extends from 3rd quadrant to 4th quadrant
x → +-∞, y → -∞
Dividing Polynomial
Long Division
1. Write both the divisor and dividend in descending powers of the variables
2. Fill any missing terms from the general form of polynomial with zeroes
3. Divide the first term of the dividend by the first term of the divisor
6x^2/2x=3x
4. Multiply the last term of quotient by the divisor, write the result below the dividend
3x*(2x+5)
5. Subtract the dividend with the product
6. Repeat steps 3-5
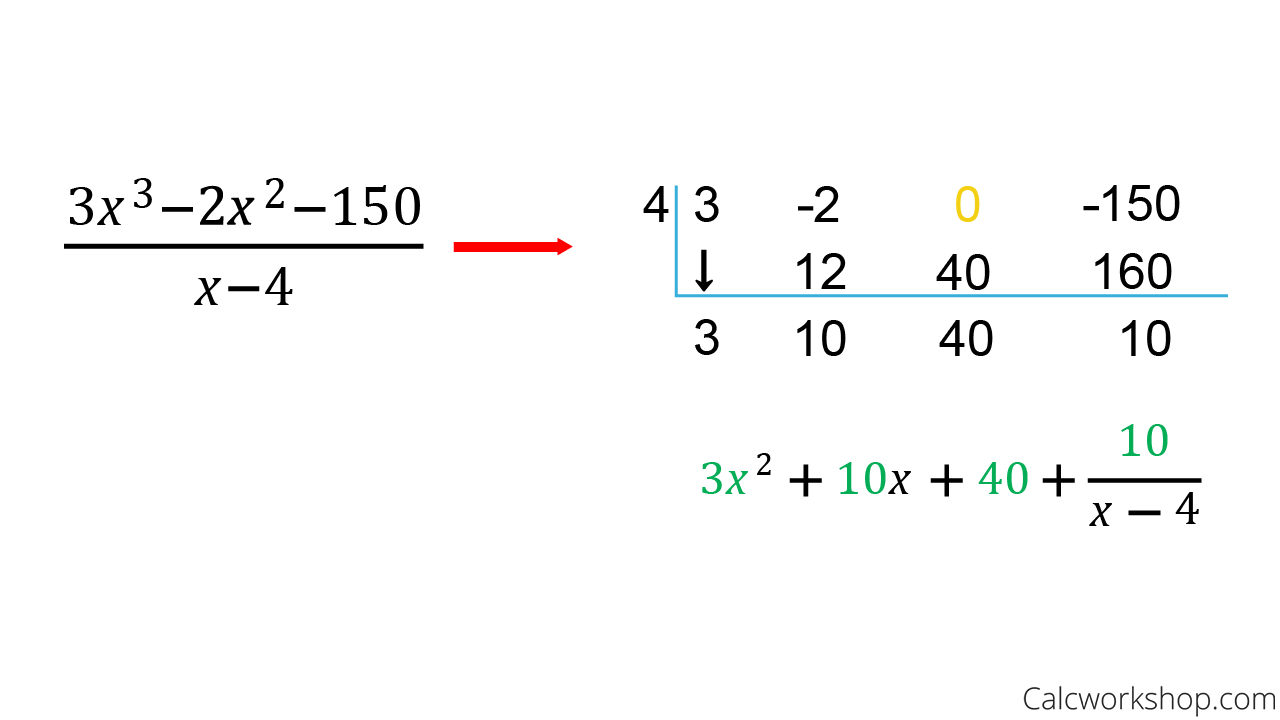
Synthetic Division
Synthetic division can only be used when the divisor is linear Ex: (x-k)
1./2. Repeat step 1 and 2 from Long Division
3. Copy the co-efficient inside the chart and place k or k/a to the left
4. Drop the first co-efficient
5. Multiply the number below the line by k. Put the product above the line in the second column and then add it with the co-efficient above it
3*4=12
-2+12=10
6. Multiply the last number below the line by k and repeat step 3-5
7. The last number(10) on the bottom row is the remainder and the rest are the co-efficient of the quotient.
Division Statement: Divisor * Quotient + Remainder
Factoring Polynomial
The Remainder Theorem
When a polynomial f(x) is divided by (x-a), the remainder is equal to f(a)
If the remainder is equal to zero, then (x-a) is a factor of f(x)
Ex: divide f(x)=x^2-4 by x-2
f(2)=(2)^2-2=0
Therefore, (x-2) is a factor of f(x) meaning remainder is 0
To factor f(x) we need to find (x-a) where f(a)=0
Possible values for "a" are the factors of the constant term (term with no variable) in f(x)
Ex: factors of 9 are +-1, +-2, +-3
Try each of them until f(a)=0
If f(a)=0, then (x-a) is a factor of f(x)
Lastly, divide f(x) by (x-a)
Factoring Sum or Difference of Cubes
a^3+b^3 = (a+b)(a^2-ab+b^2)
a^3-b^3 = (a-b)(a^2+ab+b^2)
Ex: 27x^3+125=(3x+5)(9x^2-15x+25)