Determinantes y Sistema de Ecuaciones Lineales
SISTEMAS DE ECUACIONES Y MATRICES
Sistema de ecuaciones Lineales pueden ser escritas de forma matricial y su solución se realiza usando reglas de matrices.
A * X =b A-COEFICIENTE X-INCONITA-RESULTADO
X=A∧-1 b


¿Qué son?
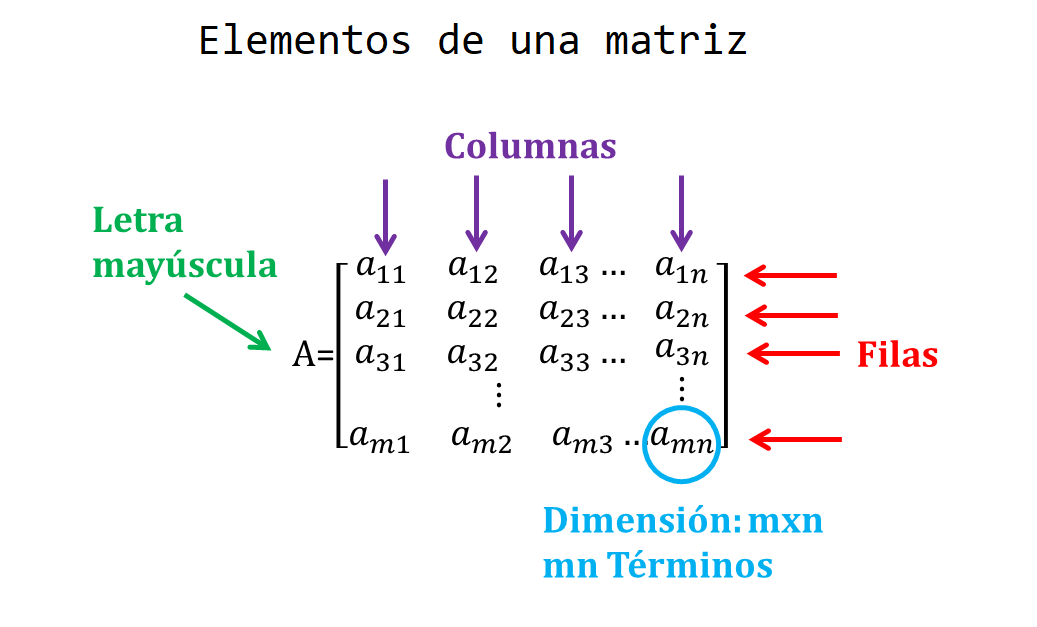
Son grupo de números ordenados, cuyas posiciones de ubicación seran dadas
EN FILAS ➡
EN COLUMNAS ⬇
a(ij)
i- elemento de la fila
- elemento de la columna
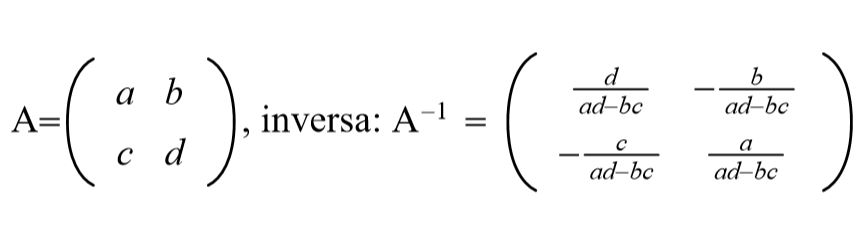
MATRIZ INVERSA
A∧-1
Matriz que resultaba matriz A y que al multiplicar su resultaba sera matriz identidad
A*A∧-1=A∧-1=A∧-1*A=I
NOTA: Matriz que no tenga inverse se denomina como no singular o invertible.
Producto de matrices
Se realiza entre vectore y la primera matriz
Vectores columba de la segunda matiz
Necesario que tengan igual dimensión
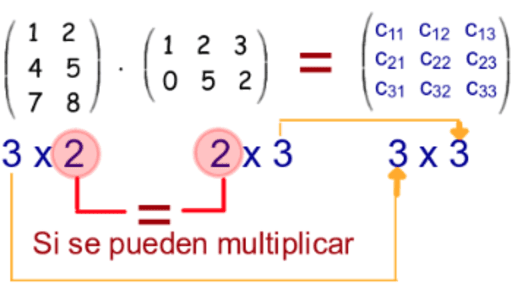
NOTA: Para realizar el producto el Nª de columnas de la 1ª matriz debe ser igual al Nª de filas de la segunda matriz
Am*n X Bn*p= Cmp
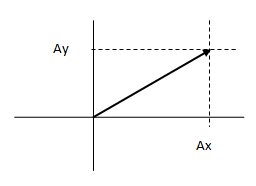
VECTORES EN 2 DIMENSIONES
V1=(Vx,Vy)=(Vc Vy)
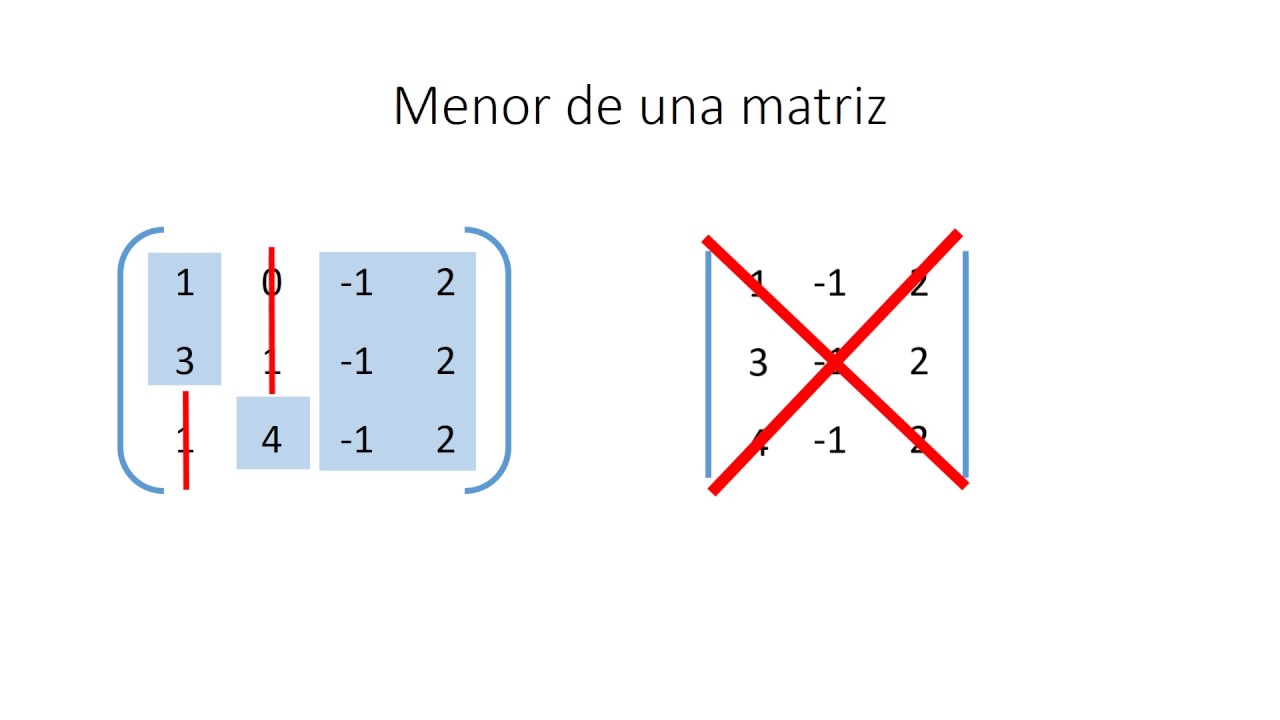
El menor (matriz)
Sub matrices por cada elemento de la matriz
Son de tamaño n-1 y m -1 en el que se elimina la fila y la columna del elemento correspondiente

COFACTOR
Con un determinante de cada multiplacdo por -1 elevado a la suma de fila y la columna
Una matriz que tenga una fila o columna de 0 su determinante es 0
Si una matriz B se obtiene al sumar o restar K veces una fila o columna de una matriz A/ Las dos matrices tienen igal determinante
Se reduce a multiplicar los elementos de la diagonal principal (+) y diagonal secundaria(-)
Aumentar las dos primeras filas o las dos primeras columnas y multiplicar los elementos de las 3 diagonales (+) y los elementos en las 3 diagonales (-)
Desarrollo de cofactores
Determinante es la suma de los productos entre los elementos de fila o columna por el cofactor determinante
La fila o columna que se debe seleccionar es la que ten mayor numero de 0, con ello evitar calcular cofactores
Se representan
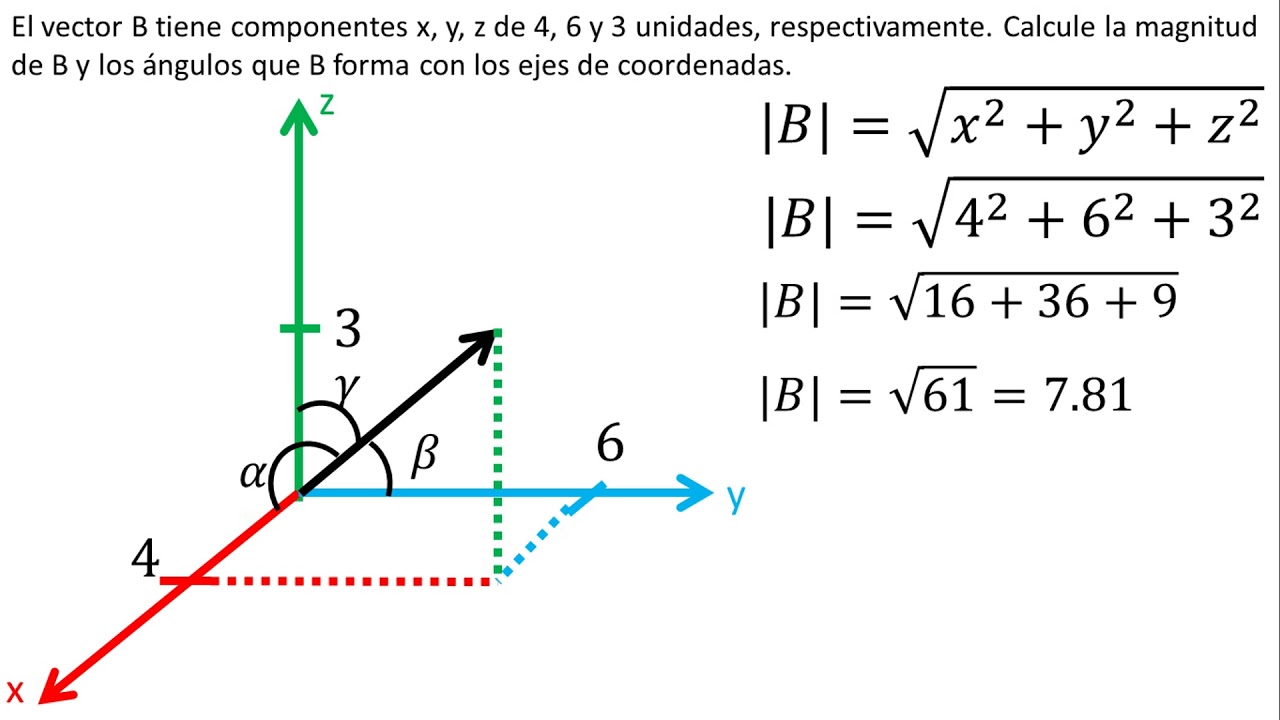
VECTORES EN 3 DIMENSIONES
w=(Wx,Wy.Wz)=(Wx,Wy,Wz)
VECTORES EN 3 DIMENSIONES
PRINCIPALES TIPOS DE MATRICES
Matriz Cuadrada
Número de filas, igual al numero de columnas
i≤j -- 1≤i≤n -- 1≤j≤n

Matriz Diagonal
Matriz cuadrada
Los elementos fuera de la diagonal son ceros

Matriz Escalar
Matriz cuadrada
Los elementos fuera de la diagonal son ceros
Iguales los que se encuentran en la diagonal

Matriz Identidad
Los elementos De la diagonal es 1 y el resto 0
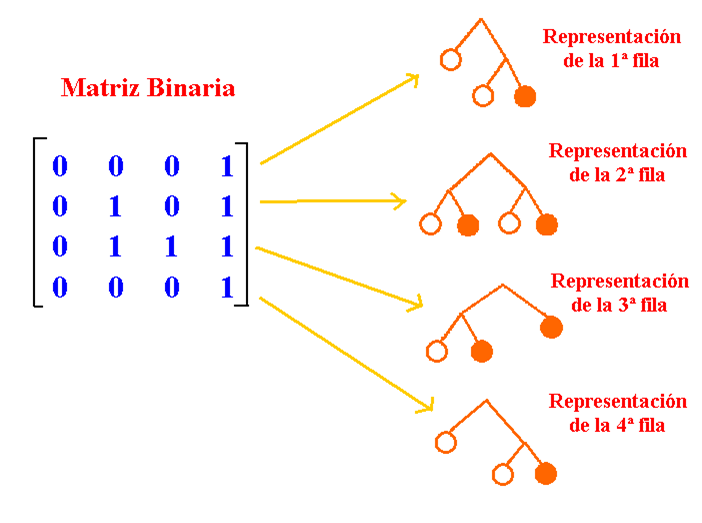
Matriz Binaria
Matriz cuyos elementos son 0 y 1

Matriz transpuesta
(A∧T)- Matriz cuyas filas se tranforman
Suma de matrices

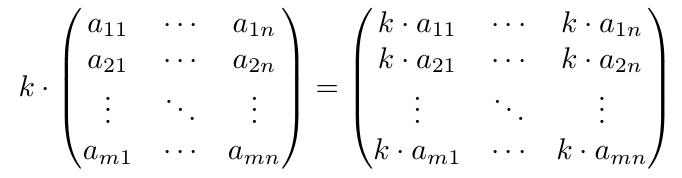
Multiplicación de una matriz por un escalar
Resultado de una matriz cuyos elementos son K veces el valor original donde K es escalar
COMBINACIÓN LINEAL DE MATRICES DE IGUAL TAMAÑO
MATRIZ AMPLIADA
Formada por la matriz de coeficiete(A) y matriz resultado (b) separados por una vertical

PROPIEDADES DE MATRICES
PRODUCTO DE ESCALARES
1) (C1+C2)A=C1A+C2A
2) C1(A+B)=C1A+C1B
3) C1(A+B)= A(C1B) = ((1A) B

PROPIEDADES DE MATRIZ TRANPUESTA
1) (A∧T)∧T=A
2) (A+B)∧T=A∧T+B∧T
3) (AB)∧T=B∧T*A∧T
4) (C1+A)∧T=C1*A∧T
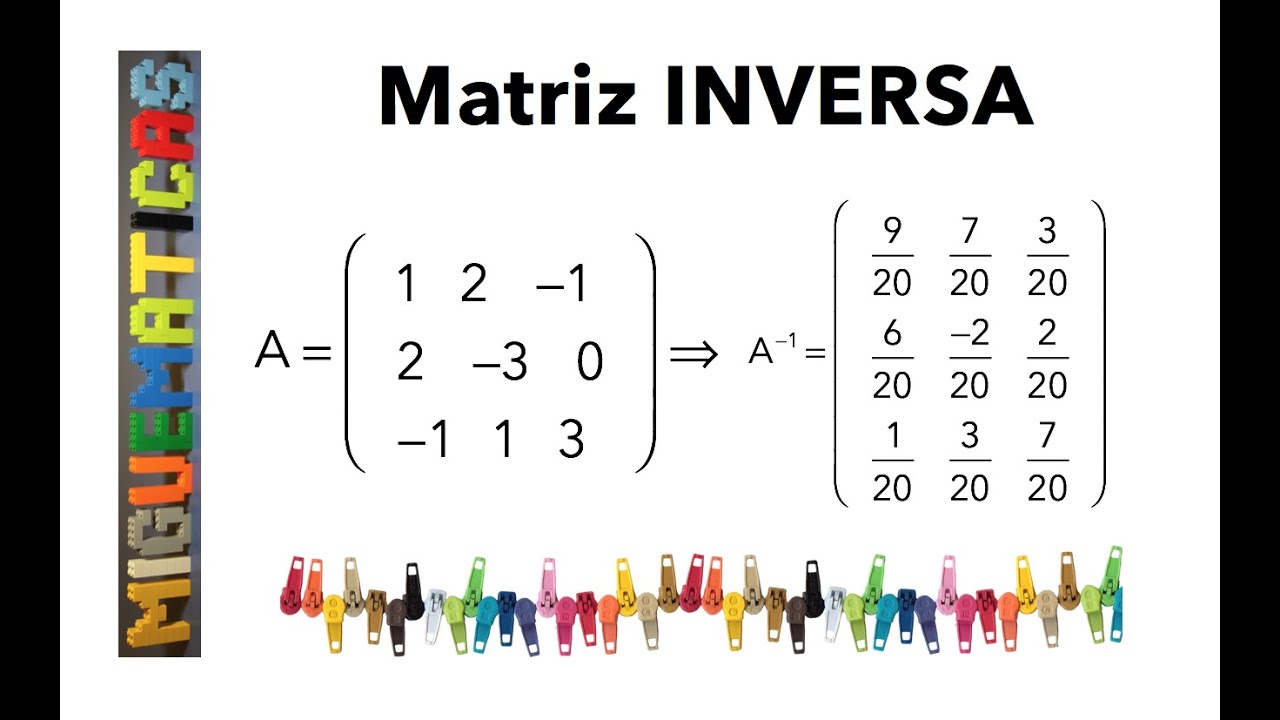
MATRIZ INVERSA
PROPIEDADES DE MATRIZ INVERSA
1) (A∧-1)∧-1=A
2) (A*B)∧-1=B∧-1-A∧-1
3) (A∧T)-1=(A∧T)∧T
FORMA DE CALCULO
Se escribre la matriz ampliada
Lado derecho de la vertical se coloca la matriz identidad
se transforma en una escalonada reducida por filas (gauss jordan)
matriz obtenida en el lado derecho es la matri inversa
TEOREMA
Una matriz B es inversa a una matriz A y si oslo si A,B= B,A =J
Si la matriz A tiene inversa(A∧ -1)entonces una matriz inversa 2, UNICA

OPERACIONES ELEMENTALES SOBRE LA MATRIZ AUMENTADA

Matriz escalonada reducida por filas
Si la matriz aumentada tiene filas con unicamente 0 deben econtrarse al final
El primer elemento diferente de 0 al leer de izqueirda a derecha debe ser 1 llamado 1 principal
El uno principal en las filas debe encontrarse abajo ya la derecha del uno principal de la fila procedente
En una columna que se encuentre el uno priincipal el resto de elementos son 0
Se puede realizar operaciones elementales sin alterar el sistema de ecuaciones
A una fila de la matriz se puede multiplicar por una constante diferente de 0
A una fila se lo puede intercambios con otra fila
A una fila cualquiera se puede sumar o restar k veces otra fila
Dependencia o Independencia Lineal

Independiente
Si las constantes son 0 son independientes
Al no existir contantes significaría que son ceros
C1,C2 = 0

Dependiente
Si las constantes son distintos de 0 son dependientes
C1,C2 ≠ 0undefined

Matriz equivalente por fila 1
Equivalentes
Si una matriz B / tamaño mxn /se obtiene mediante un numero finito de operaciones elementales./ sobre la matriz A de un tamaño mxn
Entonces dos matrices son equivalentes or filas

METODO DE GAUSS
GAUSS
Mediante operaciones elementales se obtiene una matriz escalonada por filas
Incógnitas o Variables- ultima fila y reemplazando en la fila anterior para encontrar el resto de incógnitas
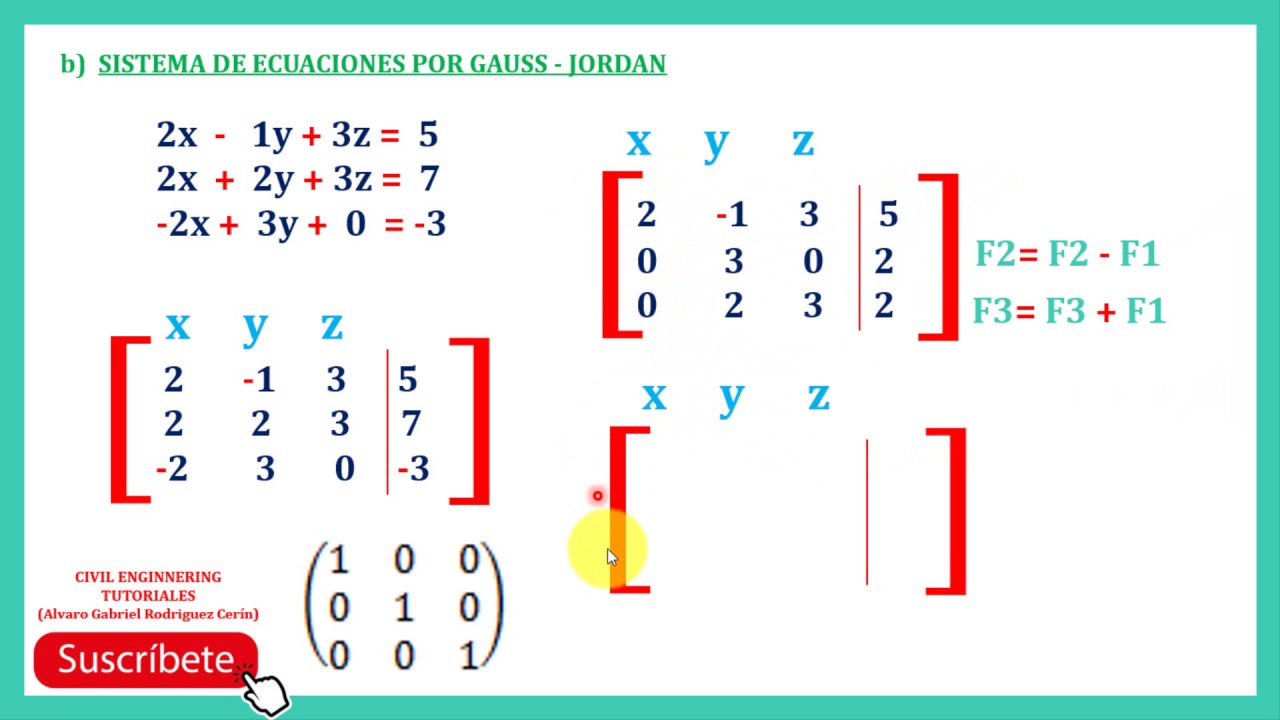
METODO DE GAUSS JORDAN
GAUSS JORDAN
Mediante operaciones elementales se obtiene una matriz escalonada reducida por filas
Incógnitas o Variables- Se obtiene de forma directa
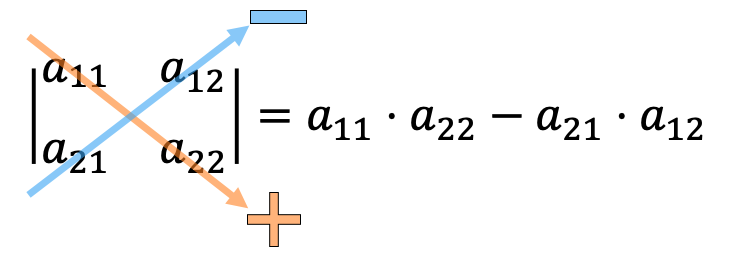
Funcion determinante
Matriz cuadrada
Convierte- en numero
Determinante de una matriz se denota con la letra de la matriz y dos rayas verticales a sus costados.
Existen reglas de calculo de 2x2 y 3x3, para matrices 4x4 existen metodos diferentes.
Una Matriz tiene dos filas o dos columnas iguales 0 multiplos entre ellos su determinante es 0
Si una matriz B se realiza intercambiendo 2 filas o 2 columnas de una matriz A, entonces det(A)=-det(B)
El determinante de una matriz triangular suoerior o triangular inferior es el producto de los elementos de la diagonal
TEOREMAS
Si un sistema de m ecuaciones y incognitas tiene como caracteristicas que m es menor que n mcn, el numero de ecuaciones es menor que el numero de incognitas entonces el sistematiene al menos una solucion
COROLARIO
El determinante de una matriz inversa es igual a la division de uno para el determinante de la matriz, siemore y cuando el determinante de la matri sea diferente de 0
TEOREMA
TEOREMA A
Si un sistema de m ecuaciones y incognitas tiene como caracteristica que m es menor que n m < n, el numero de ecuaciones es menor que el numero de incognitas entonces el tiene al menos una solucion.
Sea un sistema de ecuaciones donde m=n igual numero de ecuaciones que de incognitas
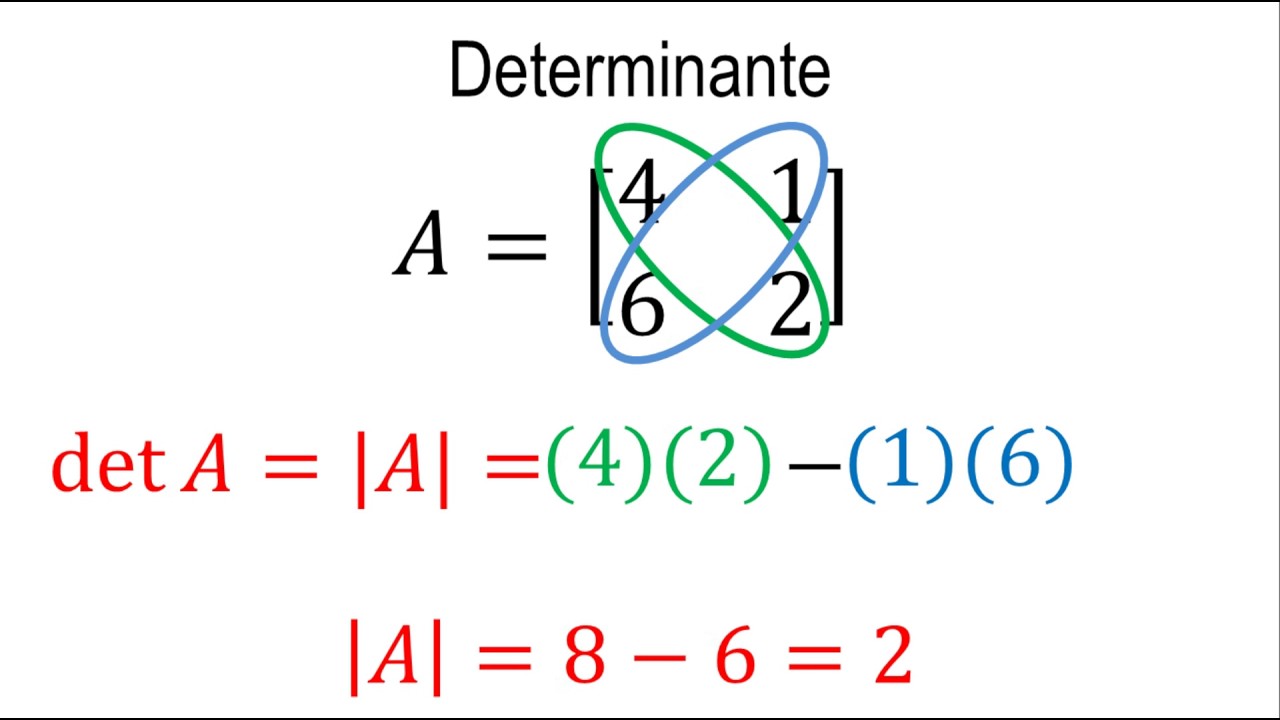
DETERMINANTES
Los deter,omamtes de una matriz cuadrada y de su traspuesta tienen IGUAL. det A = det (A∧T)
El determinante de un producto de matrices es igual al producto de los determinantes
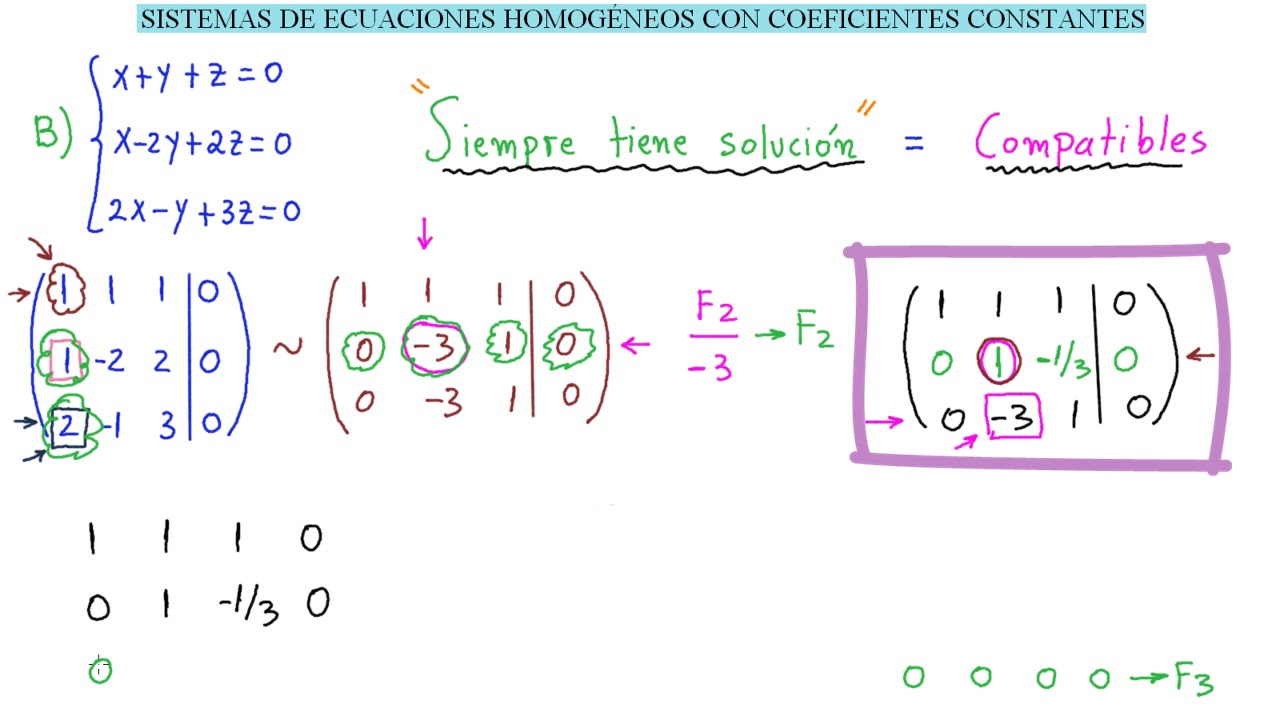
Sistemas homogeneos
Son aquellos sistemas de ecuaciones lineales cuya matriz de resultado es 0
Cunado una de las matrices sea diferente de cero sera Rango=3 -------- Caso contrario Rnago <3
El sistema de ecuaciones AX=0 tiene solucion adicional a la trivial si el m<n
m= numero de ecuaciones
n= numero incognitas

Descomposicion L*U (Factorización)
Es un metodo que se puede encontrar en algoritmo para resolver sistema de ecuaciones con igual numero de ecuaciones como de incongnitas (m=n)
El producto de U*L no dara la matriz a = L*U ≠ A
U = matriz triangular superior
L= matriz triangular inferior
El metodo consiste en descomponer o factorar la matriz A en dos matrices tiangular superior (U) y truangular inferior (L) del tal manera que A= L*U
El objetivo es encontrar la matrix X
AX=B (L*U)x=B L(UX)=B L(Z)=V

Matriz inversa usando matriz adjunta
MATRIZ ADJUNTA: Es una matriz cuadrado forma, que son los cofactores.
Adj (A)=La matriz transpuesta de la matriz de cofactores
Teoterema A: Sea una matriz cuadrada n*n y su matriz adjunta
Adj(A)*A=A*Adj(A)=det(A)I
COROLARIO-----Si la igualdad del teorema anterior multiplicamos a los dos lados por la inversa se obtiene
FORMULA
A*Adj(A)=det(A)*I
(A∧-1*A)*Adj(A)=A∧-1*det(A)*I
I*Adj(A)=det(A)*A∧-1
Adj(A)= det(A) * A-1
A∧-1=1/(det(A))*Adj (A)

Rango de una Matriz
RANGO
Es el número de filas que sea linealmente independientes
El rango es el número de filas diferente de 0
Transformar matriz a escalonada por filas


