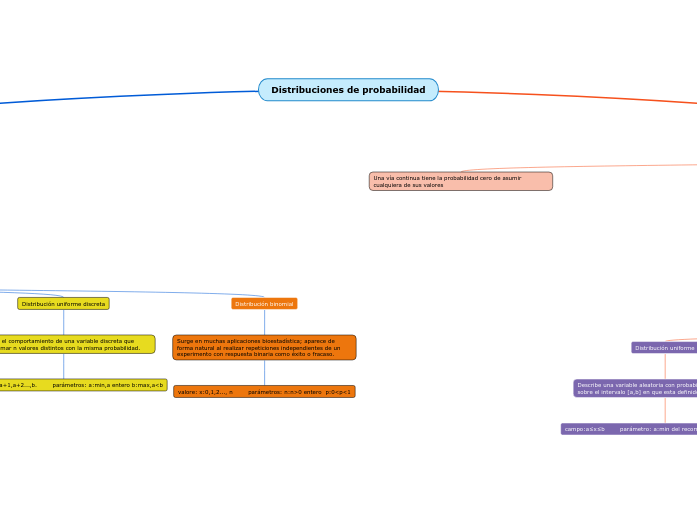
Distribuciones de probabilidad
Distribución discreta de probabilidad
Es el conjunto de pares ordenados(x,f(x) ) es una función de probabilidad de la V.a discreta x si satisface las siguientes condiciones
1) f(x) ≥ 0. 2) Σ f(x) = 1. 3) P (X=x) = f(x)
Las distribuciones discretas son
Distribución Poisson
Se puede utilizar como una aproximación de la binomial Bin (n,p)si el numero de pruebas n es grande pero la probabilidad de éxito p es pequeña
Valores: x:0,1,2 parámetro: lambda >
Distribución binomial negativa
Propuesta como una alternativa a la distribución de poisson para modelar el numero de ocurrencias de sucesos.
valores: x:0,1,2... parámetros: p:0<p<1
Distribución geométrica
Permite calcular la probabilidad de que tenga que realizarse un numero k de repeticiones hasta tener un éxito por primera vez
valores: x:0,1,2... parámetros: p:0<p<1
Distribución hipergeométrica
Aparece en proceso muestral en reemplazo, en el que se investiga la ausencia o presencia de ciertas características
valores: x:max{o,n-(N-R)}...min {R,n} parámetros: N:N>0 R:R≥0 n:n>0
Distribución uniforme discreta
Describe el comportamiento de una variable discreta que puede tomar n valores distintos con la misma probabilidad.
valores: x:a,a+1,a+2...,b. parámetros: a:min,a entero b:max,a<b
Distribución binomial
Surge en muchas aplicaciones bioestadística; aparece de forma natural al realizar repeticiones independientes de un experimento con respuesta binaria como éxito o fracaso.
valore: x:0,1,2..., n parámetros: n:n>0 entero p:0<p<1
Distribución continua de probabilidad
Una vía continua tiene la probabilidad cero de asumir cualquiera de sus valores
La probabilidad continua no puede representarse en forma tabular pero si con la siguiente formula ¨F(x)¨
Función de densidad
se construye de tal forma que el área comprendida bajo la curva es siempre igual a uno, cuando se calcula sobre todo el recorrido de la v.a x
Las distribuciones continuas son
Distribución uniforme
Describe una variable aleatoria con probabilidad constante sobre el intervalo [a,b] en que esta definido
campo:a≤x≤b parámetro: a:min del recorrido b: max del recorrido
Distribución normal
Es la distribución limite de numerosas variables como se muestra en los teoremas centrales
campo: -∞<x<∞ parámetro: Mu:-∞<Mu<∞ sigma: sigma>0
Distribución lognormal
Es utíl para modelar datos de numerosos estudios médicos
campo: 0<x<∞ parámetro: Mu:-∞<Mu<∞ sigma: sigma>0
Distribución logística
Se utiliza en el estudio del crecimiento temporal de la variable (a,b)
campo: -∞<x<∞ parámetro: a:parámetro de posición -∞<a<∞ b: parámetro de escala, b>0
Distribución exponencial
Describe proceso en los que interesa saber el tiempo que ocurre de un determinado evento
campo:0<x<∞ parámetro: lambda:tasa,lambda>0
Distribución de t de Student
Desempeña un papel importante en la inferencia estadística asociada a la teoría de muestra pequeña
campo: -∞<x<∞ parámetro: n:grados de libertad, n>0
Distribución F de Snedecor
Asociado a la normal (n,m)
campo: 0≤x<∞ parámetro: n:grados de libertad, n>0
Distribución Beta
Es posible para una variable continua que toma valores en el intervalo [0,1] lo que le hace muy apropiado para modelar proporciones
campo: 0≤x≤1 parámetro: p:p>0 q:q>0
Distribución Gama
Aparece cuando se realiza el estudio de la duración de elementos físicos (tiempo de vida)
campo: 0<x<∞ parámetro: a: a>0 p:p>0