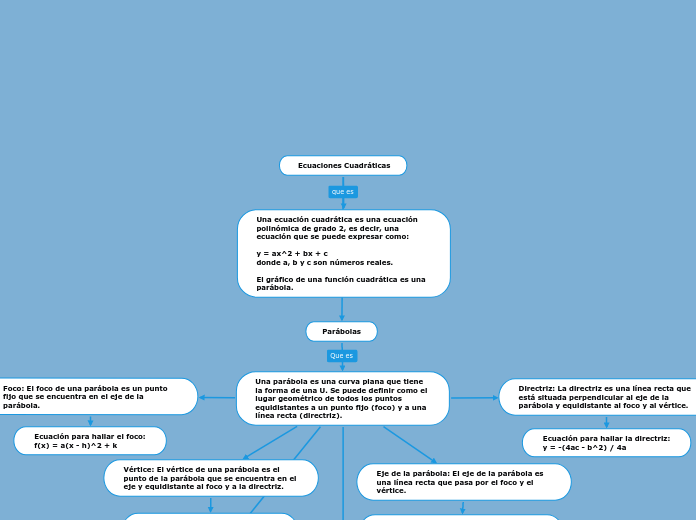
Ecuaciones Cuadráticas
Parábolas
Una parábola es una curva plana que tiene la forma de una U. Se puede definir como el lugar geométrico de todos los puntos equidistantes a un punto fijo (foco) y a una línea recta (directriz).
Foco: El foco de una parábola es un punto fijo que se encuentra en el eje de la parábola.
Ecuación para hallar el foco:
f(x) = a(x - h)^2 + k
Vértice: El vértice de una parábola es el punto de la parábola que se encuentra en el eje y equidistante al foco y a la directriz.
Ecuación para hallar el vértice:
(h, k) = (-b/2a, -(4ac - b^2) / 4a)
Eje de la parábola: El eje de la parábola es una línea recta que pasa por el foco y el vértice.
Ecuación para hallar el eje de la parábola:
x = h
Directriz: La directriz es una línea recta que está situada perpendicular al eje de la parábola y equidistante al foco y al vértice.
Ecuación para hallar la directriz:
y = -(4ac - b^2) / 4a
Ecuación canónica: y = a(x - h)^2 + k
Traslaciones y desplazamientos en el plano de una parábola
Desplazamiento vertical: Si se suma o se resta una constante a la variable y, la parábola se desplaza verticalmente hacia arriba o hacia abajo.
Desplazamiento lateral: Si se suma o se resta una constante a la variable x, la parábola se desplaza lateralmente hacia la derecha o hacia la izquierda.
Cambio en la altura: Si se multiplica la ecuación por una constante positiva, la parábola se ensancha. Si se multiplica la ecuación por una constante negativa, la parábola se estrecha.