Efecto de la ionosfera

El 12 de diciembre de 1901, Marconi consiguió realizar de forma satisfactoria la primera comunicación
radiotelegráfica transatlántica cubriendo una distancia de 3.000 km entre Gales y Terranova, en el
extremo oriental de Canadá. Unos años antes, Hertz había comprobado experimentalmente la
existencia de ondas electromagnéticas, cuya naturaleza era similar a la de la luz.

luz. Por este motivo

Exito de Marconi resultaba inexplicable considerando que las ondas electromagnéticas deben

propagarse según trayectos rectilíneos y que la esfericidad de la tierra impedía la visibilidad directa.

De hecho el éxito inicial de Marconi fue recibido con cierto escepticismo por la comunidad científica,

Que en parte dudaba de su veracidad. En el año 1902 otros experimentos realizados por Marconi

^Pusieron de relieve que las comunicaciones a grandes distancias sufrían fuertes variaciones según se

realizasen durante el día o la noche.

La propagación de ondas electromagnéticas en la ionosfera se puede modelar a partir de la propagación
en plasmas. Un plasma es una región de espacio, con la permitividad eléctrica y la permeabilidad
magnética del vacío, que contiene electrones libres. Un modelo simplificado es el de plasma frío, en el
que se desprecia el movimiento de los electrones por causas térmicas. Un análisis más acorde con la
realidad debe considerar la presencia de un campo magnético estático, de la misma manera que en la
ionosfera existe el campo magnético terrestre.

Considérense en primer lugar las fuerzas a las que se encuentra sometido un electrón inmerso
en el campo electromagnético de una onda plana.

funcionamiento

Éste experimentará una fuerza debida al campo

eléctrico y otra al campo magnético dadas por

En el análisis anterior no se ha considerado el efecto del campo magnético terrestre. Un plasma
sometido a un campo magnético constante posee características anisótropas, de forma que la constante
dieléctrica no es un escalar sino un tensor.

Tras propagarse por un medio anisótropo de espesor l con constantes de propagación k1 y k2
para cada una de las polarizaciones circulares se obtiene (despreciando las reflexiones en las
superficies de separación entre medios)

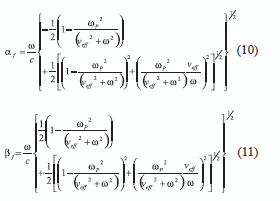
expresión de una onda polarizada linealmente con una dirección rotada respecto al eje x un
ángulo φ dado

La existencia de la ionosfera permite, tal como comprobó Marconi, las comunicaciones a grandes
distancias. El efecto de la ionosfera es distinto para las diferentes bandas de frecuencias. A frecuencias
bajas y muy bajas (bandas de LF y VLF) la ionosfera supone un cambio brusco en términos de λ del
índice de refracción atmosférico. Esta variación abrupta produce una reflexión de la onda incidente en
la parte baja de la ionosfera.

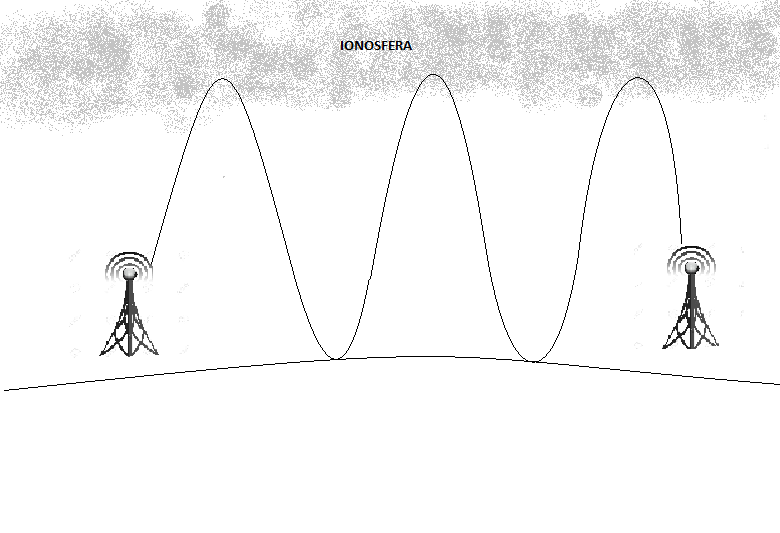
Se puede considerar que la superficie de la tierra y la parte baja de la ionosfera forman una guía
de ondas que favorece la propagación a grandes distancias en estas bandas de frecuencias (típicamente
entre los 5.000 y 20.000 km).

La condición para que la onda regrese a la tierra es que para cierta altura se cumpla, según la
ley de Snell,

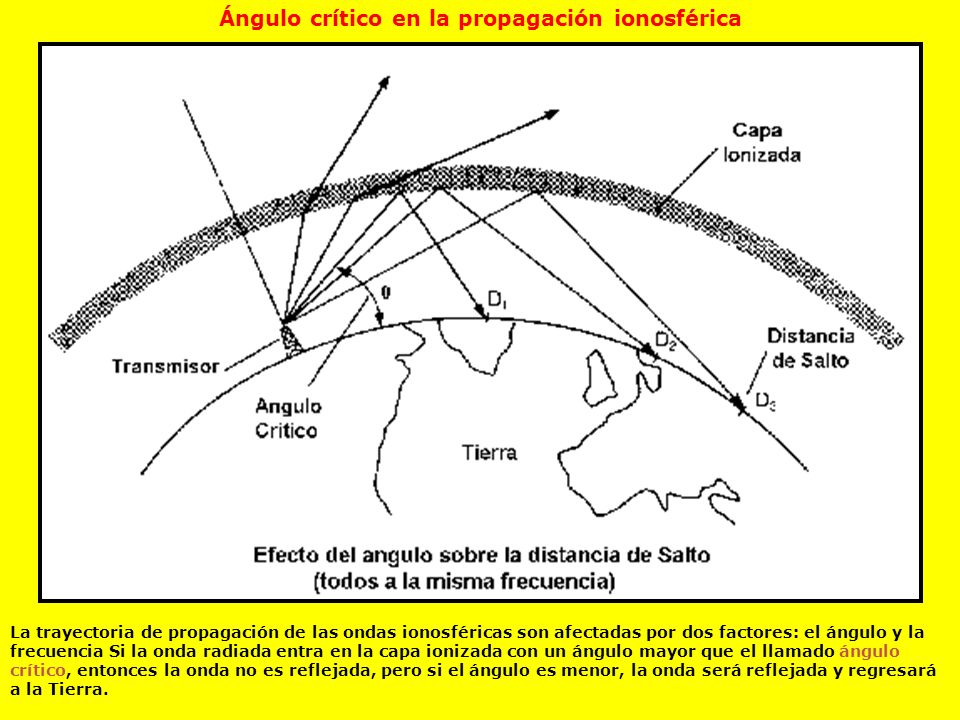
altura a la que se produce la reflexión virtual. Esta expresión supone un modelo de tierra
plana y no es válida cuando el ángulo de incidencia en la ionosfera es grande, ya que en este caso debe
considerarse el efecto de la curvatura de la tierra.

Los modelos de propagación de las secciones anteriores son útiles para evaluar las pérdidas de
propagación asociadas a los distintos efectos que se han descrito: reflexión en tierra, difracción por
obstáculos, etc. Cuando el efecto dominante en las pérdidas de propagación es únicamente uno de ellos
las permiten estimar adecuadamente.

En entornos de propagación complejos en los que existe una superposición de varios efectos, el cálculo de las pérdidas de propagación debe abordarse de forma diferentes

En la mayoría de las ocasiones no existe
visibilidad directa entre los dos extremos del enlace: la estación base y el terminal móvil.

En
función de la fase de cada una de las contribuciones la suma de todas ellas puede ser constructiva o
destructiva. En el caso de ser destructiva se producirá un fuerte desvanecimiento en la señal recibida.

Los modelos empíricos se basan en el ajuste de leyes de decaimiento de la potencia recibida en función
de la distancia, altura de antenas, frecuencia y tipología del entorno a datos medidos. Evidentemente,
mientras que ciertos parámetros como la frecuencia o la altura de las antenas son conocidos de forma
unívoca otros, como la tipología del entorno son más difíciles de objetivar.

Generalmente los modelos
empíricos distinguen entre zonas urbanas muy densas, zonas urbanas de baja densidad y zonas rurales.
A lo largo del tiempo se han desarrollado distintos modelos empíricos.

una altura de antena de la estación base de 200 m implica una variación de la forma 1/R2,98 y

para una altura de 30 m la variación en función de la distancia es de la forma 1/R3,52.

Los modelos empíricos sólo proporcionan el valor medio o esperado de las pérdidas de propagación
para un entorno genérico en función de la distancia entre la estación base y el terminal.

Sin embargo,
es evidente que aún manteniendo la distancia a la estación base constante se observarán fluctuaciones
en los niveles de señal en distintas ubicaciones del terminal móvil.

Dado que estas variaciones dependen de múltiples factores independientes,
la resultante es una variación aleatoria de distribución gaussiana. De forma que las pérdidas de
propagación

En una situación real de comunicaciones móviles el campo
incidente en la antena receptora es el resultado de la
superposición de múltiples contribuciones: campos reflejados en
edificios, campos difractados en las aristas o bordes de los
edificios, componentes reflejadadas en el suelo, y componentes
provenientes de múltiples reflexiones.

A este efecto se le denomina desvanecimiento
por multicamino, y se caracteriza estocásticamente. En la figura
2.30 se muestra un ejemplo de la potencia recibida en un
terminal móvil en función de la distancia.

En entornos urbanos
densos en que es habitual que no exista visibilidad directa entre el terminal móvil y la estación base las
fluctuaciones en la densidad de potencia incidente y por tanto en la potencia recibida se caracterizan
por una función de densidad de probabilidad Rayleigh.

receptor conectado a una antena separada una distancia d de las demás, a la salida de cada receptor
se realiza una estimación de la relación señal a ruido y a continuación se realiza un proceso de
selección o combinación. Una posibiliad es seleccionar en cada momento la salida de la rama que
presente una mejor relación señal a ruido.

De esta forma se garantiza que no se produzcan
desvanecimientos profundos simultáneamente en todas las ramas, y por tanto el empleo de la
diversidad mejorará las características globales del receptor. En un sistema de diversidad en espacio
significa que la distancia d entre antenas receptoras debe ser tal que exista independencia estadística
entre el campo incidente en cada
una de las antenas.