Exponential Functions
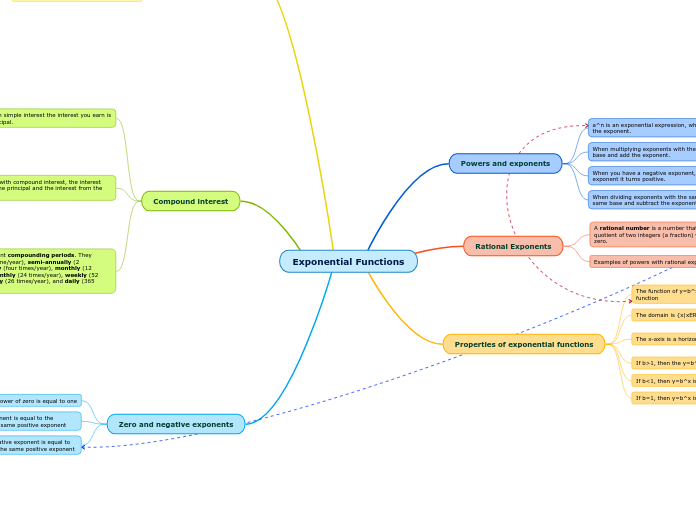
Powers and exponents
a^n is an exponential expression, where a is the base and n is the exponent.
When multiplying exponents with the same base, you keep the base and add the exponent.
For example: 2^2 x 2^2=2^4
When you have a negative exponent, you put one over the exponent it turns positive.
For example: 3^-2=1/3^2=1/9
When dividing exponents with the same base, you keep the same base and subtract the exponents.
For example: 3^6/3^2=3^4
Rational Exponents
A rational number is a number that can be expressed as the quotient of two integers (a fraction) where the divisor is not zero.
For example: 0.75, -3/4, -2.
Examples of powers with rational exponents: x^n/m
n is a natural number, x>0 when n is a even number, if x<0, n must be an odd number.
Properties of exponential functions
The function of y=b^x where b>0 defines an exponential function
The domain is {x|xER}, and the range is {y|y>0 yER}
The x-axis is a horizontal asymptote
Asymptote is a line/value that you get closer and closer to but never reach. The line of the graph gets closer and closer to the x-axis but never touches or crosses it.
If b>1, then the y=b^x is continuously decreasing
If b<1, then y=b^x is a straight line
If b=1, then y=b^x is a straight line
Power of power
When raising an exponent to a power it is just like raising a regular number to a power
When raising a power to another power the exponents get multiplied
For example: (a^3)^2= (a^3)(a^3)=a^6
Compound interest
Simple Interest: With simple interest the interest you earn is based only on the principal.
The formula for simple interest is: I=prt
I stands for simple interest, p stands for principal amount, r stands for annual rate, and t is time in years.
Compound interest: with compound interest, the interest you earn is based on the principal and the interest from the previous period.
Your principal amount for the next period is the same as your final amount for the previous period.
The formula for compound interest is A=P(1+i)^n
A is the amount of principal and interest, P is the present value of the investment or debt, i is the rate of interest per period, and t is the total number of periods
For example: $5000 is invested at 8% compounded quarterly. By looking at this statement you know that the principal amount is $5000, the interest is 0.02 (you divide the given interest by four because it is compounded quarterly), and the n value is 20 because it is compounded quarterly for five years (4x5=20). You solve this by substituting all the values into the formula, and you should get a=$7429.74.
There are many different compounding periods. They include annually (1 time/year), semi-annually (2 times/year), quarterly (four times/year), monthly (12 times/year), semi-monthly (24 times/year), weekly (52 times/year), bi-weekly (26 times/year), and daily (365 times/year).
Zero and negative exponents
Any value raised to the power of zero is equal to one
For example: 7^0=1
Any base raised to a negative exponent is equal to the reciprocal of the base raised to the same positive exponent
For example: 2^-4/3^-4=3^4/2^4
Any fractional base raised to a negative exponent is equal to its reciprocal of the base raised to the same positive exponent
For example: (a/b^-m)= b/a^m