FUNÇÕES
Formas de representar
Diagrama de setas
Neste diagrama utilizam-se setas para ligar cada um dos objetos do primeiro conjunto à sua respetiva imagem no segundo conjunto. Muito bom do ponto de vista visual, porque permite-nos ver imediatamente que objetos estão ligados a que imagens. No entanto é impraticável no caso de se tratar de um grande volume de dados.
aTabela
As tabelas que representam uma função podem ser desenhadas tanto na vertical como na horizontal. Se estiver na horizontal a primeira linha corresponde aos objetos e a segunda às imagens. Se estiver na vertical, a primeira coluna corresponde aos objetos e a segunda às imagens.
Gráfico
O gráfico de uma função corresponde a um conjunto de pares ordenados (x, y) . Neste par ordenado, à variável x corresponde o objeto, enquanto que à variável y corresponde a imagem. É muito semelhante à tabela, mas utiliza uma linguagem mais associada à matemática, em que as coordenadas dos pontos podem facilmente ser reproduzidas num gráfico cartesiano.
Gráfico cartesiano
Num gráfico cartesiano são desenhados dois eixos que se intersectam. Normalmente, ainda que isso não seja obrigatório, o eixo do x , ou seja, o das abcissas, corresponde aos objetos, enquanto que o eixo do y , ou seja, o das ordenadas, corresponde às imagens. É muito útil para se poder observar o comportamento da função.
Expressão algébrica
A expressão algébrica só pode ser utilizada para representar funções numéricas de variável numérica. Não posso utilizar uma expressão algébrica, para fazer corresponder o nome de um menino à sua idade. Apesar desta restrição, é o método que permite englobar o maior número de objetos, mesmo que estes sejam infinitos.exemplo: f(x) = 2x
Tipos de funções
Função Afim
Função Linear
Função Constante
Exemplos de funções na vida real
Definição
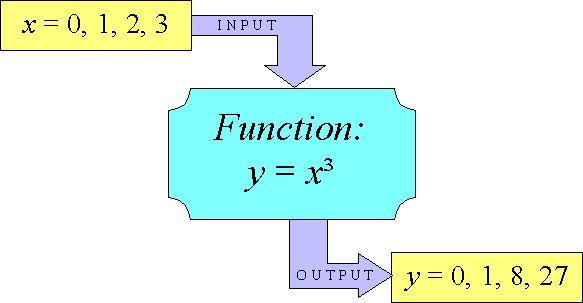
Dados dois conjuntos A e B, uma função (ou aplicação) de A em B é uma correspondência que a cada elemento x ∈ A associa um e um só elemento y ∈ B.Se f é uma função de A em B escrevemos f : A → B
Linguagem
Domínio
Estando definida a função f : A → B, o domínio da função é o conjunto A e cada um dos seus elementos designa-se por objeto.O domínio da função f representa-se por Df .Os objetos são designados por x .O x também é designado por variável independente.
Conjunto de Chegada
É o conjunto B
Contradomínio
O contradomínio da função é o conjunto formado por todos os elementos do conjunto B que se encontram "ligados" ao conjunto A. Estes elementos designam-se por imagens.O contradomínio da função f representa-se por C.D. ou D´As imagens são designadas por y ou f (x) .O y também é designado por variável dependente.