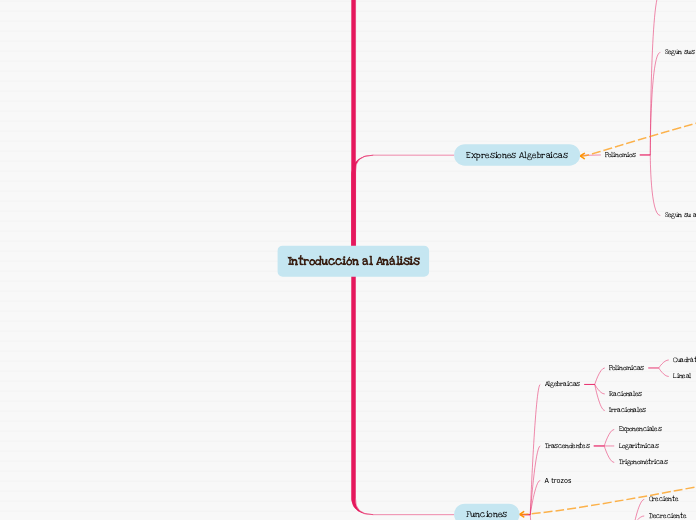
Introducción al Análisis

Números Reales (R)

Números Racionales (Q)

Conjunto de fracciones equivalentes

Clasificación

Exactas

Periódicas Puras

Periódicas Mixtas

Conjunto de números enteros (Z)

Clasificación

Naturales (N)

Ceros

Negativos

Números Irracionales (I)

No pueden ser expresados como fracción

Polinomios

Según sus grados

Polinomio de primer grado

Polinomio de segundo grado

Polinomio de tercer grado

Según sus términos

Monomio

Binomio

Trinomio

Cuatrinomio

Según su análisis

Podemos aplicar

Factoreo

Factor común

Factor común en grupo

Trinomio cuadrado perfecto

Cuatrinomio cubo perfecto

Diferencia de cuadrado

Teorema de gauss

Teorema del resto

Regla de rufini

Operaciones

Suma

Resta

Multiplicación

División

Valor numérico

Grado

Termino principal

Coeficiente principal

Algebraicas

Polinomicas

Cuadrática

Lineal

Racionales

Irracionales

Trascendentes

Exponenciales

Logarítmicas

Trigonométricas

A trozos

Análisis

Gráfico

Creciente

Decreciente

Continua

Discontinua

Analítico

Dominio e Imagen

Inyectiva

Suryectiva

Biyectiva

Intervalo de Crecimiento y Decrecimiento

Conjunto de Negatividad y Positividad

Máximo y Mínimo

Conjunto de Ceros

Potenciación

Multiplico por si misma la base, tantas veces como indique el exponente.

Características

Producto de potencia de igual base o de igual exponente

Potencia de otra potencia

División de potencia de igual base o de igual exponente

Radicación

Dados dos números: Radicando e Índice, se halla un tercero llamado: Raíz

Características

Raíz de un producto de igual o distinto índice

Raíz de una raíz

Raíz de un cociente de igual o distinto índice

Notación científica

Nos permite expresar distintas cantidades con mayor facilidad en forma de potencia

Racionalización

Elimina las raíces del denominador

Operaciones con radicales

Adicion y Sustraccion

Radicales semejantes

Radicales no semejantes

Multiplicación

Igual índice

Distinto índice

División

Igual índice

Distinto índice

Racionaliza los denominadores

Eliminar radicales del denominador

Radical

Suma o diferencia de raices cuadradas

Suma o diferencia de un número real y un cuadratico

Inducción

Razonamiento que permite demostrar proposiciones que dependen de una variable n que toma una infinidad de valores enteros

La demostración está basada en el axioma denominado Principio de la inducción matemática.

Binomio de Newton

Convierte un binomio a cualquier potencia de exponente N

Observación

Los exponentes de a disminuyen en 1 y los de b aumentan en 1

La suma de los exponentes en cada término es igual al exponente de (a+b) elevado a la n

Permutación, Variación y Combinatoria

Importa el orden

Si

Participan todos los elementos

Si

Se repiten los elementos

Si

Variacion con repeticion

No

Variación

No

Se repiten los elementos

Si

Permutacion con repeticion

No

Permutacion

No

Participan todos los elementos

No

Se repiten los elementos

Combinación con repetición

Combinación

Logaritmo

Exponente al que hay que elevar un número, llamado base, para obtener otro número determinado.

Clasificación

Logaritmo Decimal

Base 10

Logaritmo Natural o Neperiano

Base N° e

Propiedades

Logaritmo de base

Logaritmo de unidad

Multiplicación de igual base

Dividion de igual base

Logaritmo de una potencia

Logaritmo de una raíz