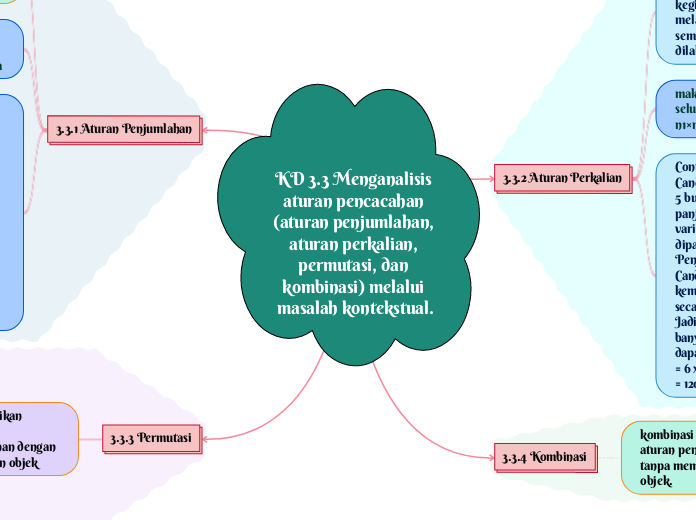
KD 3.3 Menganalisis aturan pencacahan (aturan penjumlahan, aturan perkalian, permutasi, dan kombinasi) melalui masalah kontekstual.

Misalkan, ada n1 cara melakukan kegiatan 1, n2 cara melakukan kegiatan 2, ..., nk cara melakukan kegiatan k, dimana semua kegiatan tersebut dilakukan bersamaan

maka banyak cara melakukan seluruh kegiatan adalah:
n1×n2×n3×...×nk

Contoh :
Candra mempunyai 6 buah kaus, 5 buah kemeja dan 4 buah celana panjang. Tentukan banyaknya variasi pakaian yang dapat dipakai Candra?
Penyelesaian:
Candra dapat memakai kaus, kemeja, dan celana panjang secara bersamaan.
Jadi, dengan aturan perkalian banyak variasi pakaian yang dapat dipakai Candra adalah:
= 6 x 5 x 4
= 120 variasi

kombinasi merupakan suatu aturan pencacahan/penyusunan tanpa memperhatikan urutan objek.

Ernest Hemingway - The Old Man and the Sea

Misalkan, ada n1 cara melakukan kegiatan 1, n2 cara melakukan kegiatan 2, ..., nk cara melakukan kegiatan k, dimana semua kegiatan tersebut tidak dapat dilakukan bersamaan.

maka banyak cara melakukan seluruh kegiatan adalah: n1+n2+n3+...+nk; n=banyak cara

Contoh :
Sultan memiliki 3 mobil, 2 sepeda motor dan 4 sepeda. Berapa cara Sultan dapat ke kantor dengan kendaraannya?
Penyelesaian:
Perhatikan bahwa Sultan hanya dapat menggunakan salah satu kendaraan (tidak dapat menggunakannya bersamaan).
Jadi, dengan aturan penjumlahan banyak cara Sultan pergi ke kantor dengan kendarannya adalah:
3 + 2 + 4 = 9 cara.

Permutasi dapat diartikan sebagai aturan pencacahan/penyusunan dengan memperhatikan urutan objek

faktorial dari bilangan asli

Subtopic

Permutasi dati unsur-unsur yang berbeda

Subtopic

Permutasi yang memuat unsur yang sama

Subtopic

Permutasi siklis

Subtopic