Measurement Project Concept Map
Pythagorean Theorem
Pythagorean Theorem: a^2 + b^2 = c^2
The Pythagorean Theorem Is an equation devided to find the length of the slope opposite the 90 degree angle in right triangles. A^2 + B^2 = C^2 is the relationship in length between the sides of the triangle.

For this example lets suppose that A=5 and B=12.
To solve for C: Plug in the numbers you can into the equation A^2 + B^2 = C^2. Since we know A and B we can plug those in, gic=ving you 5^2 + 12^2 = C^. This can be simplified to be 169 = C^2. Taking the square root of both 169 and C^2 you are left with the answer: C = 18.
Geometric Figures
Angles
Angle Measure
Supplementary angles
when the sum of two
angles measure
180 degrees
Complimentary angles
when the sum of two
angles measure 90
degrees.
Congruent angles
when two angles
have the same
exact measure
Vertical angles
Two nonadjacent angles
formed by two
intersecting lines
Classification of angles
Alternate- Interior- Angles
Alternate-exterior-Angles
Corresponding angles


The sum of angle measures in Triangles
the sum of all angles in
a triangle is 180 degrees.
Classification of Polygons
Types of Triangles
Classification by angle measure
Acute
Right
Obtuse
Classification by side lengths
Scalene
Equilateral
Isosceles
Types of Quadrilaterals
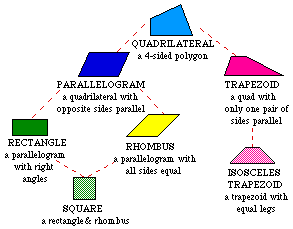
Circles
Regular Polygons
polygons that include
some degree of symmetry
How to find the measures of a Polygon
Prisms and Pyramids
Prisms
right prism
oblique prism

Pyramids

Surface Area Polyhedrons
Surface area: The total area of the surface of a three-dimensional object
Polyhedrons are the 3-D shapes that are made up of several flat faces. Some Examples are in the Pyramids and Prisms section.
Surface Area Equations
Prism: 2B + ph
Pyramid: B + (1/2)ph
Key: B=Area of th base, p=Perimeter of the base, h=height

For this example the height(h) is 4, the length(L) is 5 and the width(w) is 3.
The first thing that needs to be done is finding the area and perimeter of this shape's base. The perimeter of the base is 2(5) + 2(3)= 16 = p The Area of the base is 5 x 3 = 15 = B Remember our equation for finding the surface area of prisms is 2B + ph. Since we know all the variables we can plug them in now. 2(15) + 16(4) - 30 + 64 - 94 u^2 = Surface area
Main topic
Volume of Polyhedrons
Volume is the measure of the space inside a three-dimentional figure.
Polyhedrons are the 3-D shapes that are made up of several flat faces. Some Examples are in the Pyramids and Prisms section.
How to find the volume of Polyhedrons
Prisms: The area of the base multiplied by the height. Equation: B x h B=Area of base h=height
Pyramids: One third of the area of the base times the height. Equation: (1/3) x B x h B=Area of base h=height
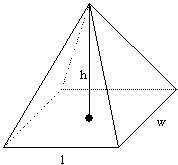
For This Example h=5, w=4, L=6
The first thing we have to do in order to solve this problem is to fing the area of the base. To do that we need to multiply Lxh. 6x4=24. 24 is now B. Remember the equation to find the volume of pyramids is (1/3)xBxh=V. we can now plug in B and h and proceed to find the volume. (1/3)x24x5 is what our equation looks like now. multiplying that out gives us 40. 40 u^3 is the volume of this pyramid
Area and Perimeter
Area
TRAPIZOID
To find the area of a trapizoid you take the sum of the bases and then multiply by the height of the trapizoid, and then you divivde the number by two. Viola!
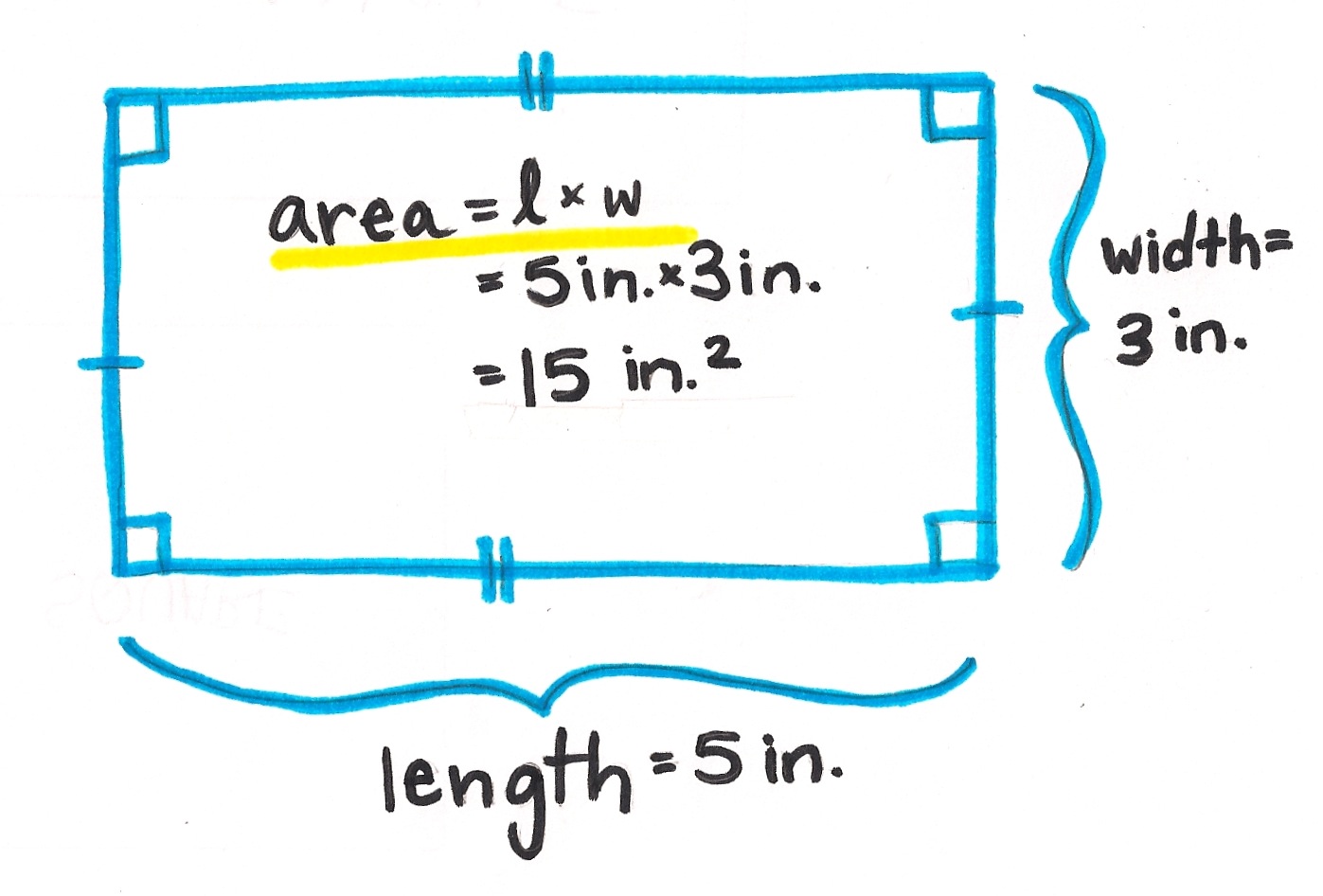
RECTANGLE
To find the area if a rectangle you multiply length times width
CIRCLE
To find the area of a circle you use the formula
Area=pie*diameter or if you just have the radius then the formula is Area=pie*radius*radius
Perimeter

TRIANGLE
To find the perimeter of a triangle you simply add up all of the sides if all of the sides lengths are given. If on the other hand the triangle has a missing sign you then use the pythagorean Theorem which looks like this
A2+B2=C2
CIRCLE
To find the perimeter of a circle you use the formula
Circumfrence= Pie*diameter or Circumfrence=Pie*Radius *radius
SQUARE
To find the peimeter of a square all you have to do is multiply what ever number is shown for the sides by four because all of the sides on a square are the same size.
