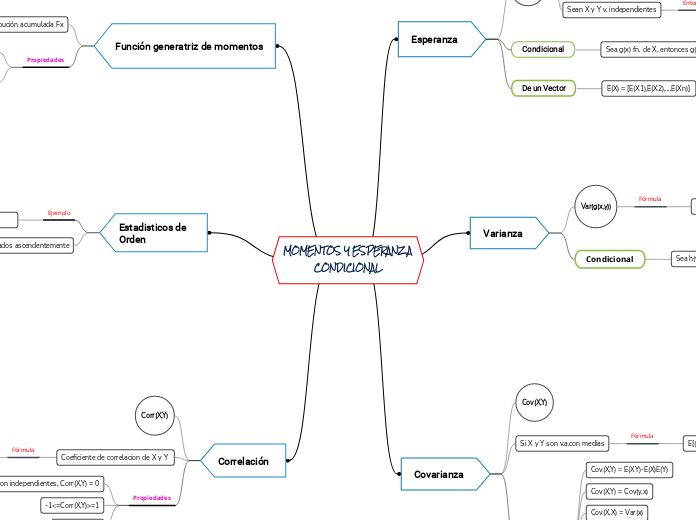
MOMENTOS Y ESPERANZA CONDICIONAL
Esperanza
Eg(x,y)
∑_x∑_y〖g(x,y)f(x,y)〗; caso discreto
∬_(-∞)^∞〖g(x,y)f(x,y)〗, caso continuo
Sean X y Y v. independientes
Entonces
E[g(x)h(y)] = E[g(x)] E[h(y)]
Condicional
Sea g(x) fn. de X, entonces g(x) dado Y=y
E[g(x)|Y=y]
Fórmulas
∑_x〖g(x)f(X|Y=y)〗
∫_(-∞)^∞〖g(x)f(X|Y=y)〗
De un Vector
E(X) = [E(X1),E(X2),...,E(Xn)]
Varianza
Var(g(x,y))
Fórmula
E[g(x,y)-Eg(x,y)]^2
Condicional
Sea h(y) fn. de Y, entonces h(y) dado X=x
Var(h(y)|X=x)
Fórmula
E[h^2(y)|X=x]-E^2[h(y)|X=x)
Covarianza
Cov(X,Y)
Si X y Y son v.a.con medias
Fórmula
E[(X-μx)(Y-μy)]
Propiedades
Cov(X,Y) = E(XY)-E(X)E(Y)
Cov(X,Y) = Cov(y,x)
Cov(X,X) = Var(x)
Cov(c,X) = 0
Cov(X1+X2,Y) = Cov(X1,Y)+Cov(X2,Y)
Cov(cX,Y) = cCov(X,Y)
Si X y Y son independientes, Cov(X,Y) = 0
En general, Cov(X,Y) = 0 =/ X,Y independientes
Función generatriz de momentos
Si X es una v.a. con fn. de distribución acumulada Fx
Entonces
Mx(t)=E(E^xt)
Propiedades
La n-derivada de la fn. generatriz de momentos es :
M_x^n (t) = E(e^xt x^n)
La n-derivada de la fgm evaluada en t=0 es:
M_x^n (t=0) = E(x^n)
Estadisticos de Orden
Ejemplo
x ̃= 1/n ∑_(i=1)^n〖Xi,S^2 〗= 1/(n-1) ∑_(i=1)^n〖(Xi-x ̃)〗^2
Son valores demostrados ascendentemente
X1,X1,...,Xn
Correlación
Corr(X,Y)
Coeficiente de correlacion de X y Y
Fórmula
Cov(X,Y) / √(Var(x)Var(y))
Propiedades
Si X y Y son independientes, Corr(X,Y) = 0
-1<=Corr(X,Y)>=1
|Corr(X,Y)| = 1