MTE 280: Elementary Mathematics
Cornell Notes
How to properly take good, clear notes in Mathematics that you can easily study from for upcoming exams.
This website (hyperlink attached) goes through step by step how to use the Cornell Note taking style.

Colored Pens
By using different colored pens it allows the student to catch their mistakes easier. If each step they write is in a different color then it is much easier for them to identify that mistake because they can clearly see what they did wrong. The teacher could come over and simply say "look over your work in the color green," then they will see what they did wrong and correct it quicker than if everything was in one color.

Commutative Property of Addition/Multiplication
Refers to moving stuff around. For addition, the rule is "a + b = b + a"
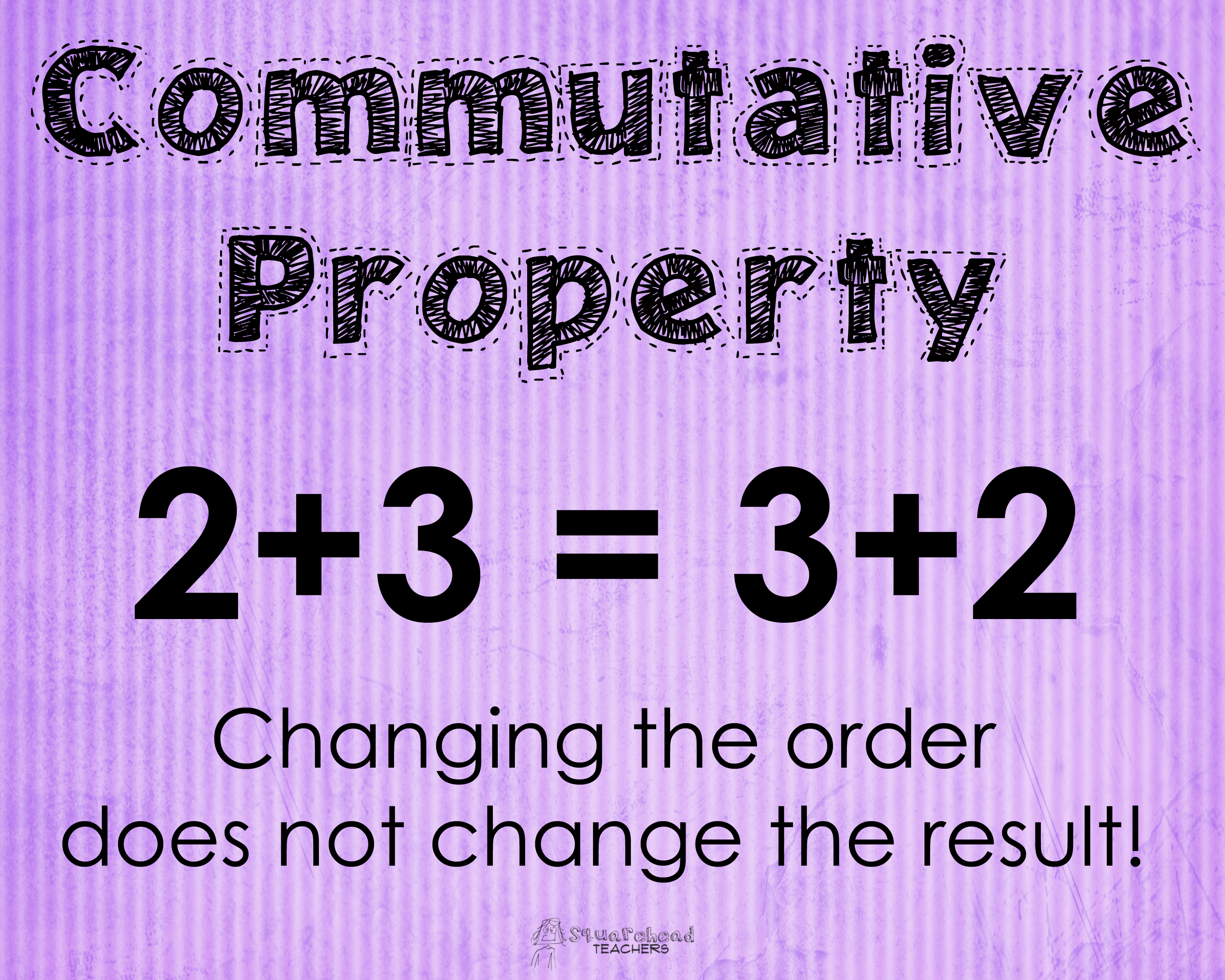
Converting from Base Ten to Base Five
Using the "upside down" division method. The answer must be less than the number five.

Divisor
The thing doing the dividing

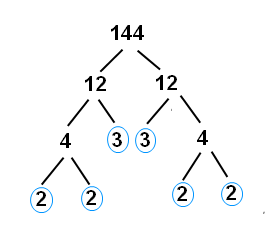
Prime Factorization
Only prime numbers being multiplied
Modeling Integers: Diagram
Modeling Integers: Missing Addend
Multiplying Integers
Decimals & Fractions
Dividing Fractions
Exponent Rules
Juggling Lesson
This lesson was meant to teach the students that if you don't practice something, you will never learn it. By just showing the students how to juggle, it wasn't allowing them to throughly learn the concept and therefore the students weren't able to properly do it.

Looking For a Pattern
When doing math problems always look for patterns that you can use. Students learn better if they have something to follow, such as a pattern. For example, when teaching exponents to students they will see that any number raised to the power of one will always be the original number (10^1=10, 5^1=5), or when any number is raised to the power of zero the number will always be one (10^0=1, 5^0=1). These are a few of the patterns that can be used in mathematics.

Associative Property of Addition/Multiplication
You can add or multiply regardless of how the numbers are grouped. By 'grouped' we mean 'how you use parenthesis'.

Finding Different Methods to Add/Subtract/Multiply
Using repetition, punnett squares, Chinese method, etc.

Prime
Exactly 2 factors

Composite
More than 2 factors