Potenciación y Radicación
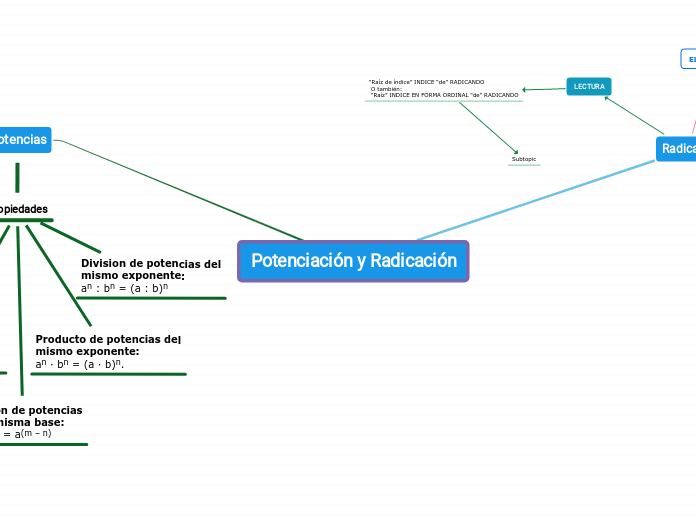
Potencias
Definición
Es un producto entre factores iguales
Eementos
Exponente: numero de veces
que se multiplica la base
Base: Factor que se multiplica
por sí mismo
Nomenclatura:-'base' elevado a
'exponente'
- 'base' al 'nombre ordinal del exponente.
Propiedades
Potencias especiales
Exponente 0: son iguales a 1
Exponente 1: son iguales a la base
Base 0: son iguales a la base
Base 1: Son iguales a la base
Potencia de una potencia:
(am)n = a(m·n)
Producto de potencias
de la misma base:
am · an = a(m+n)
Division de potencias
de la misma base:
am : an = a(m – n)
Producto de potencias del
mismo exponente:
an · bn = (a · b)n.
Division de potencias del
mismo exponente:
an : bn = (a : b)n
Radicales
La raíz enésima de un número es aquel otro que elevado a un exponente n nos da dicho
número.
ELEMENTOS
- Radicando : Es el número al que se le quiere hallar la raíz. Se coloca debajo del radical.
-Raíz: Es el resultado de la operación.
-Índice: Es el número al que hay que elevar la raíz para que nos dé el radicando.
El índice 2 no se expresa
-Resto : Es la parte sobrante del radicando al que no se puede calcular la raíz. Es la
diferencia que hay entre el radicando y la raíz elevado a su índice.
PROPIEDADES
Propiedad fundamental de la raíz cuadrada: En toda raíz cuadrada se cumple que el radicando es igual a la suma del cuadrado de la
raíz más el resto.
RADICANDO = (RAÍZ)2 + RESTO
√20 = 4 ; r = 4 => 20 = 42 + 4 = 16 + 4 = 20undefinedundefined
Raíz cuadrada de un producto: La raíz cuadrada de un producto es igual al producto de las raíces cuadradas de los
factores.
√a · b = √a · √b √100 = √4 · 25 = √4 · √25 = 2 · 5 = 10
Raíz cuadrada de un cociente: La raíz cuadrada de un cociente es igual al cociente de las raíz cuadrada del dividendo
entre la raíz cuadrada del divisor.
√a ∶ b = √a ∶ √b √16 = √64 ∶ 4 = √64 ∶ √4 = 8 ∶ 2 = 4undefinedundefined
LECTURA
“Raíz de índice” INDICE “de” RADICANDO
O también:
“Raíz” INDICE EN FORMA ORDINAL “de” RADICANDO
Subtopic