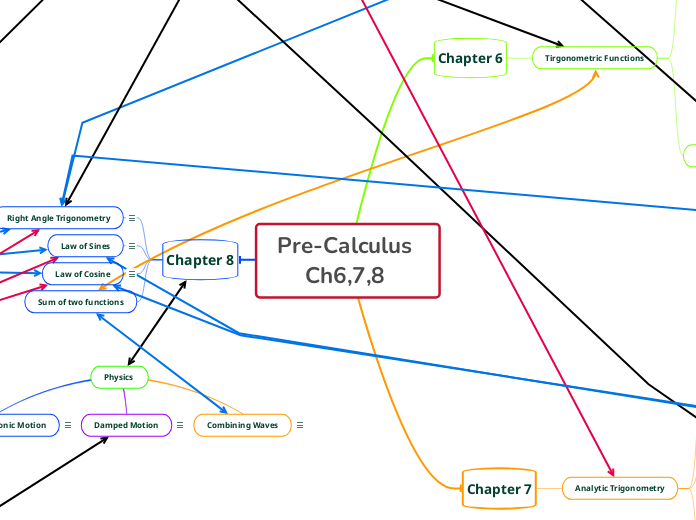
Pre-Calculus Ch6,7,8
Chapter 6
Tirgonometric Functions
Unit Circle Approach
Angles and their measure
360 degrees
Right Angle
Terminal Side
Initial side
Vertex
Decimal and Degree, minute, second form
Radian Form
Radians
Arc of a circle
conversion from radians to degrees
Area of a circle
Area of a sector
The 6 Trigonometric Functions
Amplitude
Period
Phase Shift
Sinusoidal Functions
Chapter 7
Analytic Trigonometry
Inverse of Sin, Cos, Tan
Trigonometric Equations
Identities
Quotient
Reciprocal
Pythagorean
Even-Odd
Trigonometric Formulas
Sum and Difference of Sin, Cos, Tan
Double-Angle
Half-Angle
Product-Sum
Sum-Product
Chapter 8
Right Angle Trigonometry
Law of Sines
Law of Cosine
Sum of two functions