Problem Solving- Melody
Models for Addition (story problems)
SET Model: no action performed in the problem, 2 seperate pieces
MEASUREMENT/LINE/ACTIVE: some sort of action occurs

Subtopic
Addition and Subtraction
Most commonly showed with "sets" or Venn diagrams

Venn diagram
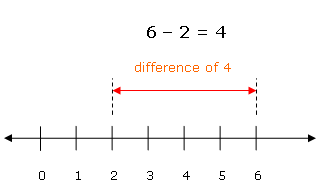
Number lines can be essential for children to understand problems.
allows for conceptual understanding, which is essential for learning
Different methods of problem solving work for different people as long as you can explain your method, and have the correct answer it's not "wrong" the most essential thing is that you understand the problem.
Drawing a picture isn't immature or childish, but one of the best ways to understand problems, even "simple" ones.
Visual hands on learning (drawing pictures, using manipulatives, number line)=good
Addition and Subtraction With Time and Money
easiest way is to use a number line

Subtopic
Methods For Subtraction
Traditional

Subtopic
Partial Sums/Differences

Subtopic
Decomposing

Subtopic
Compensating

Subtopic
Adding/Finding the Distance
52-37
37+3=40
40+10=50
50+2=52
(3+10+2)=15
Holy Shift
When you subtract using a number line
if you shift the numbers to a friendlier
position (ie. from 37 and 55 to 40 and 55)
it's easier to solve the problem.
Subtopic
Working With Different Bases (Addition)
Time
Base of 60 Instead of typical base of 10
5:15-3:45=1:30 (base is 60, have to carry enough over from other place values to have enough minutes)
Learning when to carry over when working with bases other than 10
Examples
(Base 3) 22+12=322-can't go over 2, just like you can't go over 9 with a base of 10
(Base 7) 46+31=110-can't go over 6 because the base is 7
Working With Different Bases (Subtraction)
Essentially the same as addition, just have to remember how much much to carry over
(Base 7) 62-35+24-When adding to the one place of 62 just have to remember to add seven instead of ten
5 Methods of Addition
Traditional

Subtopic
Partial Sums/Instructional Algorithm

Subtopic
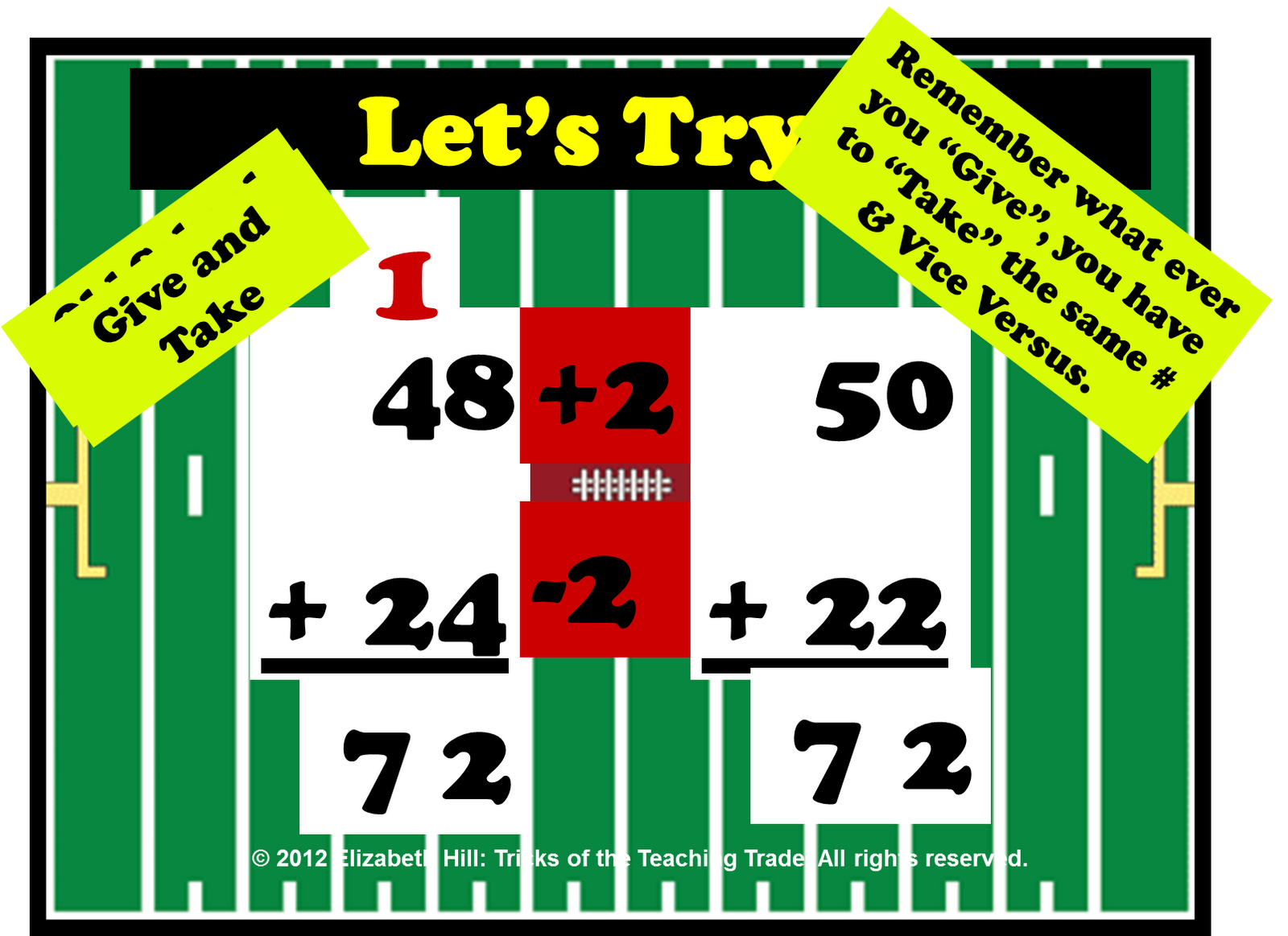
Give and Take
Subtopic
Compensating

Subtopic
Decomposing
34
+28
=
12(4+8)
+50 (30+20)
=62
Number Relationships
Spatial Relationships
recognizing how many of something there are w/out counting, by seeing the visual pattern
One and Two More, One and Two Less
knowing which numbers are one more or two less than any given number
Benchmarks of 5 and 10
10 is an essential numbers, must know how any given number relates to ten
Part-Part Whole
to conceptualize a number as being made up of 2 or more parts is the MOST important relationship to develop

Subtopic
Properties of Addition
Commutative Property
numbers in problems are movable to make problems
"more friendly"
8+7=7+8
Associative Property
can use multiple properties to move or "group" terms to make more sense
(8+7)+3=8+(7+3)
Identity Property of Zero
number stays the same value (itself) when you add zero
a+0=a
Using number lines, or a visual ALWAYS easier than algebra (for most people)

Math: All about relationships, that's why you can always find an answer.
That's why you can ALWAYS find an answer
The basic method for solving simple problems that most of us were taught isn't necessarily the best.
can be very difficult to solve problmes in your head using this method