Quadratic Functions
Forms of Quadratic Equations
What are Quadratics and Properties of Parabolas
Quadratic, a latin word for square. A quadratic is a math problem in which a variable is squared.
Parabola
A symmetrical U-shaped curve on graph representing a quadratic function
Zeroes
Also called roots are the x-intercepts of the parabola
Can have one, two or zero roots
Axis of Symmetry
A vertical line that divides the parabola into two equal halves
Axis of Symmetry is the sum of the roots divided by two
Y-intercept
The co-ordinate where the parabola crosses the y-axis
Optimal Value
The lowest or highest value/peak or bottom of the parabola depending on the a value - UPWARD or DOWNWARD?
Finite Differences in Quadratic Relations
Table of Values
FD = Subtracting consecutive y-values
If First Differences are constant, there is a linear relation

SD = Subtracting FD values
Solving Quadratic Equations
Factoring
Used to turn a quadratic into factored form to solve equation by finding X-intercepts
Finding what to multiply together to get an expression
Trinomial Standard Form
ax^2+bx+c
----------------------------
2x^2+10x-12
=2(x^2+5x-6)
=2(x^2-1x+6x-6)
=2(x(x-1)+ 6(x-1)
=2(x-1)(x+6)
1. Common Factor (If Any)
Common Factor = 2
Monomial Common Factor
12 x^2y-9x^3y^2z+18x^2y^2
_________________________
3x^2y
=3x^2y(4-3xyz+6y)
Identify greatest common factor = 3x^2y
Move GCF outside of bracket
Divide each term by the GCF and write what remains in bracket
Binomial Common Factor
2(x+1)-3y(x+1)
_____________
(x+1)
= (x+1)(2-3y)
3. Find Two integers that multiply to "c" and add to "b"
m*n=-6
m+n=-5
-1*6=-6
-1+6=5
These two integers end up being (x-r) and (x-s) in factored form
Sub. in these numbers for b value
4. Factor by grouping
If the trinominal cannot be common factored and the a value is more than 1, you have to multiply a and c
m(n)=a(c)
m+n=b
x-1=0 x+6=0
x=1 x=-6
Perfect Square Trinomials
Same method of factoring is used as factoring trinomials except you write the product as the square of a binomial
a^2±2ab+b^2 = (a±b)^2
4x^2+12x+9
4(9) = 36
m(n)=36 m = 6
n+n=12 n = 6
Sub. in numbers as bx term = 12x
=4x^2+6x+6x+9
=2x(2x+3)+3(2x+3)
=(2x+3)(2x+3)
=(2x+3)^2
1. Factor out the GCF by dividing it with all terms
2. Move GCF outside of bracket
3. Multiply a value and c value
-Find two numbers that multiply to the product of a(c) and have the sum of b
4. Substitute the two numbers for the middle term
5. Group the terms with common factors and factor each binomial group
6. The last two binomials should be the same and so you simplify them together by writing the product as the square of the binomial
E.g. (2x – 3)(2x – 3) = (2x – 3)^2
Using this as a reference equation find out what a and b are
a^2 = 4x^2 so a=√4x^2 = 2x
b^2 = 9 so b=√9 = 3
Check that "2ab" is the middle term
2ab = 2(2x)(3)
= 4x(3)
= 12x
Therefore, 2ab is the middle term and that means it is a square trinomial
First and last terms are perfect squares
Difference of Squares
Identifying Characteristics
Contains Binomials (2-terms)
Contains a difference (Subtraction)
Contains Perfect Squares
a^2 - b^2 = (a+b)(a-b)
Ax^2+Bx+C
=144p^2+0x-81
=144p^2-81
=(12p+9)(12p-9)
Using this as a reference equation find out what a and b are
a^2 = 144p^2 so a = √144p2 = 12p
b^2 = 81 so b = √81 = 9
Sub. in a and b into reference equation to get factored
Completing the Square
Convert Standard Form to Vertex Form and find Maximum/Minimum values or vertex of parabolas
y=3x^2-12x-5
y=(3x^2-12x)-5
y=3(x^2-4x)-5
-4/2=-2^2=4
y=3(x^2-4x+4)-5
y=3(x^2-4x+4)-17
y=3(x-2)^2-17
Vertex = (2,17) Minimum = -17
1. Put brackets around ax^2+bx terms
2. Common Factor the "a" value
3. Make Perfect Square Trinomial inside bracket using: (b/2)^2
4. Add the opposite sign of the (b/2)^2 inside the bracket
EX. 2(x^2+6x+9-9)+11
5. Move the opposite sign (b/2)^2 value outside bracket by multiplying it by "a" value
6. Add this value with the k value outside bracket to get final k value
7. Keep the "a" value outside bracket and square root the first term x^2, keep the sign of the middle term (addition or subtraction) and square root the last term in bracket, add a square outside of end bracket to give you: (x-h)^2
8. Write out the final Equation that is left over
Quadratic Equation
Finding x-intercepts from Standard Form using Quadratic Formula
X-intercepts/Roots/Zeroes = Solutions
x = -b ± √b^2 - 4ac
________________
2a
2=-3x^2+4x+2
a=-3, b= 4, c= 2
2. Sub in a, b, and c values in formula
3. Solve for x1
4. Repeat except make the addition sign between -b and square root subtraction
5. Solve for x2
1. Make sure L.S or R.S is equal to 0
0=-3x^2+4x+2
(b^2-4ac)
Discriminant
Positive discriminant = 2 roots
If discriminant is zero there is 1 root
Negative discriminant = no real roots
Expanding Quadratic Functions
Vertex
The point where the axis of symmetry and the parabola meet at its maximum or minimum value

Optimal Value is the Y-Value of the vertex
Axis of symmetry on the x-axis is the x-value of the vertex

Maximum point if the parabola opens downward (point with highest y-value)

Minimum point if the parabola opens
upward (point with lowest y-value)
If Second Differences are constant, there is a quadratic relation

If FD or SD are not constant, the relation is niether
Standard Form
y = ax^2 + bx + c
a, b and c are all known values
a value cannot be 0
x is the unknown variable
c value is the y-intercept of parabola
Formula for Axis of Symmetry
--------------------
x = -b/2a
y=0.5x^2-2x-6
a=0.5 b= -2 c= -6
x= 2/2(0.5)
x= 2/1
x= 2
Factored Form
y = a(x-r)(x-s)
Binomials (x-r) and (x-s) gives the x-intercepts
Solve each binomial individually for x to get the x-intercept(s)
y=0.5(x-6)(x+2)
--------------------------
x-6=0 x+2=0
x=6 x=-2
x1= (6,0) x2= (-2,0)
adding x-intercepts and then dividing by 2 = axis of symmetry - midpoint of x-intercepts
axis of symmetry is the x value of the vertex
(6,0) and (-2,0)
------------------
=[6+(-2)]/2
=[4]/2
=2
Axis of Symmetry
is (2,0)
X value of vertex
is 2 - (2,y)=vertex
Sub in axis of symmetry as x value to find optimal value (y value of vertex)
y=0.5(x-6)(x+2)
y=0.5(2-6)(2+2)
y=0.5(-4)(4)
y=0.5(-16)
y=(-8)
Optimal Value of parabola
is -8, meaning the y-value
of the vertex is -8
Sub in x as 0 to find y-intercept
y=0.5(x-6)(x+2)
y=0.5(0-6)(0+2)
y=0.5(-6)(2)
y=0.5(-12)
y=(-6)
Y-intercept is (0,-6)
Vertex Form
y = a(x-h)^2 + k
h = x value of the vertex and axis of symmetry
"h" represents a horizontal shift
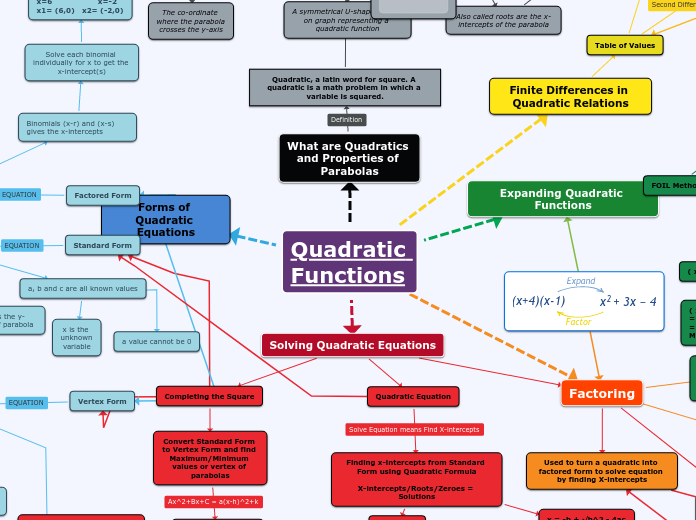
If h>0, it is a horizontal shift to the right. If h<0, it is a horizontal shift to the left
"h" value is subtracted
k = y value of the vertex
"k" represents a vertical shift

If k>0, it is a vertical shift up by k units. If k<0, it is a vertical shift down by k units.
"k" value is added
Sub in x=0 to find y-intercept
Base Parabola is
y=x^2
Vertex
---------------------------------------
(Axis of Symmetry, Optimal Value)
(x, y)
(2, -8)
Vertex
(h,k)
a = vertical stretch/compression factor
If a > 1 or a < -1, then the graph is stretched vertically by a
factor of a

If -1 < a < 0 or 0 < a < 1, (a is a fraction)then the graph is compressed vertically
Direction of Opening
-----------------------
If a>0 it is upward opening parabola, if a<0 it is downward opening parabola

Use Step Pattern for plotting points of parabola
Step Pattern
--------------
1,3,5,7,9,....
Multiply a value and step pattern to get correct points of a given parabola
Ex. a=2 Step Pattern
=2[1,3,5,7,9]
=2,6,10, 14, 18


2. Factor by Grouping (if necessary)
Group terms with common factors to solve
2x^2+6y+4x+3xy
=2x^2+4x+6y+3xy
=2x(x+2)+3y(2+x)
=(x+2)(2x+3y)
a^2 - b^2 = (a+b)(a-b)
144p^2 - 81 = (12p+9)(12p-9)
(12p+9)(12p-9) is a factored difference of squares
Expanding Binomials
(a + b)(c + d)
= ac + ad + bc + bd
e.g. (x + 4)(x – 3)
= x^2 – 3x + 4x – 12
= x^2 + x – 12
Perfect Square Trinomials
( x + a )^2 = x^2 + 2ax + a^2
( x – a )^2 = x^2 – 2ax + a^2
When the Binomial is square, to expand you must multiply the binomial by itself
( x + 5 )^2
= ( x + 5 ) ( x + 5 )
= x^2 + 10x + 25
1. Get rid of the square sign and have the binomials multiply eachother
( x – 3 ) ( x – 3 )
2. Use FOIL Method
Difference of Squares
( x + a ) ( x – a ) = x^2 – a^2
( x + 5 ) ( x – 5 )
= x^2 – 5x + 5x – 25
= x^2 – 25
Middle term cancel out
Sub. in x and a values to expand
x^2-5^2
=x^2-25
Distributive Property
a(b + c)
= ab + ac
e.g.
2(x + 4)
= 2x + 8
FOIL Method
First Outside Inside Last
( x + 3 ) ( x + 2 )
= x^2 + 2x + 3x + 6
= x^2 + 5x + 6