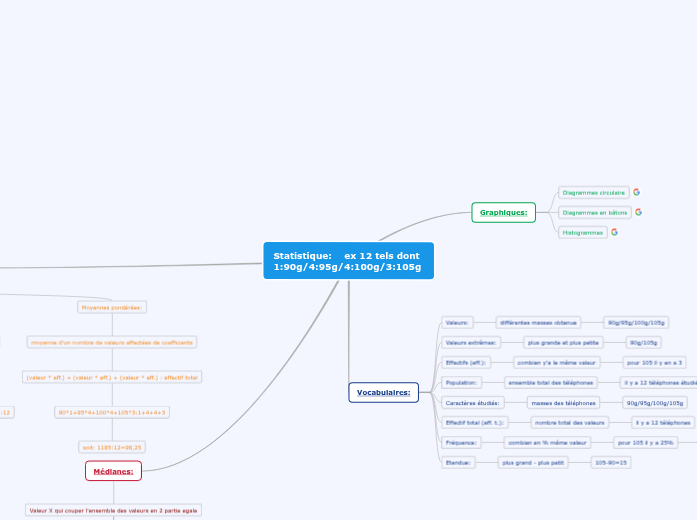
Statistique: ex 12 tels dont 1:90g/4:95g/4:100g/3:105g
Graphiques:
Diagrammes circulaire
Diagrammes en bâtons
Histogrammes
Vocabulaires:
Valeurs:
différentes masses obtenue
90g/95g/100g/105g
Valeurs extrêmes:
plus grande et plus petite
90g/105g
Effectifs (eff.):
combien y'a le même valeur
pour 105 il y en a 3
Population:
ensemble total des téléphones
il y a 12 téléphones étudiés
Caractères étudiés:
masses des téléphones
90g/95g/100g/105g
Effectif total (eff. t.):
nombre total des valeurs
il y a 12 téléphones
Fréquence:
combien en % même valeur
pour 105 il y a 25%
12(eff. t.):3(eff. 105)*100
Etendue:
plus grand - plus petit
105-90=15
Moyennes:
Moyennes de goupe:
moyennes de 2 moyennes avec des effectifs totaux différents
(moyennes 1 * eff. t. 1 + moyenne 2 * eff. t. 2) : effectif total
(98,25*12 + 17*19) : (12 + 19)
1508:31=48,64
Moyennes:
quotient de la somme des valeurs par leurs nombre
toutes les valeurs divisé par l'effectif total
(90+95+95+105+100+100+105+95+100+105+95+100):12
soit: 1185:12=98,25
Moyennes pondérées:
moyenne d'un nombre de valeurs affectées de coefficients
(valeur * eff.) + (valeur * eff.) + (valeur * eff.) : effectif total
90*1+95*4+100*4+105*3:1+4+4+3
soit: 1185:12=98,25
Médianes:
Valeur X qui couper l'ensemble des valeurs en 2 partie egale
Effectif pair
ranger croissant, couper en 2 parties de même valeurs
1;4;7;8;9;11 (40:2=20)
1;4;7;8 (1er groupe=20) 9;11 (2ème groupe=20)
donc la médiane est entre 8 et 9
8,5
Effectif impaire
ranger croissant, total-1, couper en 2 parties de même valeurs
1;4;7;8;10;11 (41-1/40:2=20)
1;4;7;8 (1er groupe=20) 10:11 (2ème groupe=21)
2ème a 1 en plus donc le premier nombre est le médian
10