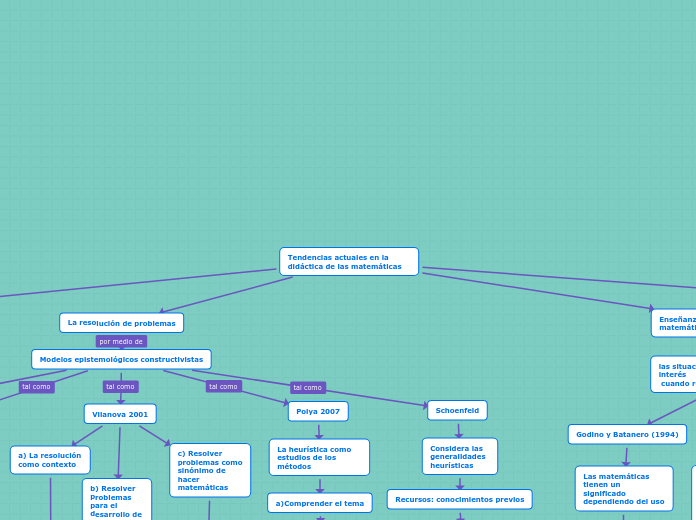
Tendencias actuales en la didáctica de las matemáticas
La Educación Matemática como proceso de inculturación.
Se trata de ayudar a los estudiantes a desarrollar la experiencia matemática mediante el cultivo de actitudes matemáticas y la estructuración de algunos conocimientos básicos.
el estudiante debe ser imbuido de ciertos hábitos y actitudes matemáticas.
La resolución de problemas
Modelos epistemológicos constructivistas
Alsina 2007
Trabajar la realidad a través de ideas y conceptos matemáticos
A partir del contexto deben crearse esquemas,
formular y visualizar los problemas, descubrir relaciones y regularidades
Forma deductiva
Vilanova 2001
a) La resolución como contexto
Justificación para enseñar, motivar y desarrollar
b) Resolver problemas para el desarrollo de habilidades
Técnicas de resolución como contenido
c) Resolver problemas como sinónimo de hacer matemáticas
Estrategias para visualizar problemas y soluciones
Guzmán 2007
intención de transmitir de una manera sistemática los procesos de pensamiento
eficaces en la resolución.
manipular objetos matemáticos
Activación de la metacognición
Polya 2007
La heurística como estudios de los métodos
a)Comprender el tema
b)Concebir un plan
c)Ejecución del plan
d)Visión retrospectiva
Schoenfeld
Considera las generalidades heurísticas
Recursos: conocimientos previos
Control: El alumno monitorea el proceso y las estrategias adecuadas
Sistema de creencias: creencias matemáticas de alumnos ayudan a concebir correctamente las estrategias
Enseñanza contextualizada de las matemáticas
las situaciones didácticas resultan de mayor interés
cuando recuperan la cotidianidad.
Godino y Batanero (1994)
Las matemáticas tienen un significado dependiendo del uso
El alumno necesita tener noción práctica significativa
Alsina (2007)
La matemática como útil para la interpretación y modelización de la
realidad, capaz de sorprender y emocionar y necesaria para la toma de decisiones ciudadanas.
Proenza y Leyva (2006)
El papel del profesor
Brousseau (2000) sugiere que los maestros trabajen en formular, esquematizar,
visualizar problemas basados en la realidad próxima.
debe tener un componente científico, un
conocimiento práctico de los medios adecuados de transmisión de las actitudes y
saberes de la actividad matemática.