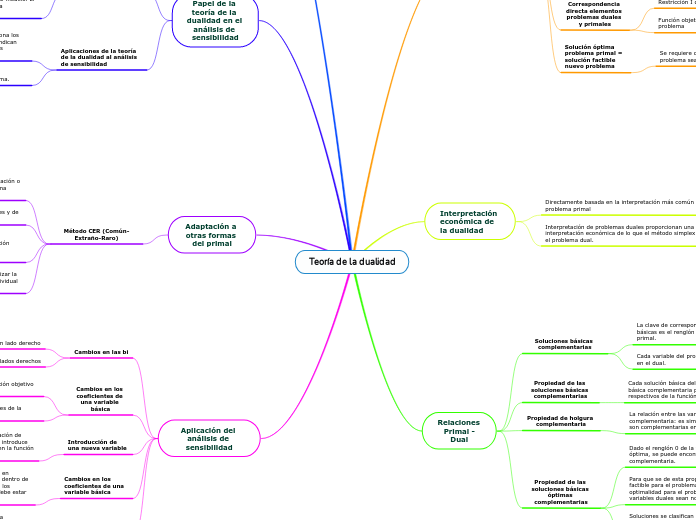
Teoría de la dualidad

Problema dual = solución problema primal (satisfacer prueba de optimalidad)

Iguales parámetros problema dual y primal

Coeficientes de función objetivo del problema primal = lados derechos de las restricciones funcionales del problema dual

Lados derechos de las restricciones funcionales del problema dual primal = coeficientes de la función objetivo del problema dual.

Coeficientes de una variable de las restricciones funcionales del problema primal = coeficientes de una restricción funcional del problema dual.

Correspondencia directa elementos problemas duales y primales

Restricción I de un problema = variable I del otro problema

Función objetivo de un problema = lados derechos del otro problema

Solución óptima problema primal = solución factible nuevo problema

Se requiere que el valor mínimo factible de W en el nuevo problema sea minimizado

Directamente basada en la interpretación más común del problema primal

Interpretación de problemas duales proporcionan una interpretación económica de lo que el método simplex hace en el problema dual.

Llegar a solución BF que satisfaga los requisitos sobre el uso provechoso de los recursos (estos comprenden la condición de optimalidad del algoritmo)

Soluciones básicas complementarias

La clave de correspondencia directa entre las soluciones básicas es el renglón de la tabla simplex de la solución básica primal.

Cada variable del problema primal tiene una variable asociada en el dual.

Propiedad de las soluciones básicas complementarias

Cada solución básica del problema primal tiene una solución básica complementaria para el problema dual, donde los valores respectivos de la función objetivo (Z y W ) son iguales.

Propiedad de holgura complementaria

La relación entre las variables de la solución básica primal y dual complementaria: es simétrica, es decir, las dos soluciones básicas son complementarias entre sí.

Propiedad de las soluciones básicas óptimas complementarias

Dado el renglón 0 de la tabla simplex de la solución primal óptima, se puede encontrar la solución dual óptima complementaria.

Para que se de esta propiedad, la solución dual debe ser factible para el problema dual, ya que la condición de optimalidad para el problema primal requiere que todas las variables duales sean no negativas.

Soluciones se clasifican según cumplan con que todas las variables de la solución aumentada son no negativas (condición de factibilidad) o cuando todos los coeficientes del renglón 0 son no negativos (condición de optimalidad).

Análisis de sensibilidad

Objetivo fundamental: identificar los parámetros sensibles

Parámetros sensibles (no pueden cambiar sin que cambie la solución óptima)

Parámetros no clasificados como sensibles: determinar el intervalo de valores del parámetro para el que la solución óptima no cambia.

Utilizado para problemas grandes, en vez de realizar el simplex nuevamente

Procedimiento para análisis de sensibilidad

Revisión del modelo: hacer cambio deseados

Revisión de la tabla simplex final

Conversión a la forma apropiada de eliminación de gauss

Probar factibilidad: se verifican todas las variables básicas de la columna del lado derecho

Probar optimalidad: verificar si la solución es óptima (factible)

Reoptimización

Análisis de sensibilidad

Cambios en los coeficientes de una variable no básica: el cambio en sus coeficientes no puede afectar la factibilidad de la solución.

Introducción de una nueva variable: la inclusión de otra variable equivale a introducir una nueva variable al modelo. El único cambio que resulta en el problema cual es la introducción de una nueva restricción.

Aplicaciones de la teoría de la dualidad al análisis de sensibilidad

Precios sombra: la solución optima dual proporciona los precios sombra de los recursos respectivos que indican cuanto puede cambiar z si se hace cambios en las cantidades de recurso.

Método simplex dual: se utiliza cuando se desea reoptimizar para identificar la nueva solución optima.

Método CER (Común-Extraño-Raro)

Formular problema primar de cualquier forma, maximización o minimización. el dual quedara automáticamente en forma contraria.

Determinar si cada forma de las restricciones funcionales y de las restricciones es c, e o r.

Para cada restricción sobre una variable individual en el problema dual, usar la forma que tiene la misma condición que la restricción funcional en el problema primal correspondiente a la variable dual.

Para cada restricción funcional en el problema dual, utilizar la misma condición que la restricción sobre la variable individual correspondiente del problema primal.

Cambios en las bi

Intervalo permisible para un lado derecho

Análisis de cambios simultáneos en los lados derechos

Cambios en los coeficientes de una variable básica

Intervalo permitido para un coeficiente de la función objetivo de una variable no básica

Análisis de cambios simultáneos en los coeficientes de la función objetivo

Introducción de una nueva variable

Para considerar una nueva actividad que la formulación de programación lineal no haya tomado en cuenta, se introduce un nueva variable con los coeficientes apropiados en la función objetivo y en las restricciones del modelo actual.

Cambios en los coeficientes de una variable básica

Suponiendo que una variable xj (con j fija) que está en estudio es una variable básica de la solución optima dentro de la tabla simplex final. los únicos cambios se realizan los coeficientes de esta variable. aquí la tabla simplex debe estar en la forma apropiada de eliminación de gauss.

Introducción una nueva restricción

Luego de obtener una solución, introducir una nueva restricción. esto puede ocurrir si se pasó de alto la restricción en un principio o porque hayan surgido nuevas consideraciones después de formular el modelo.