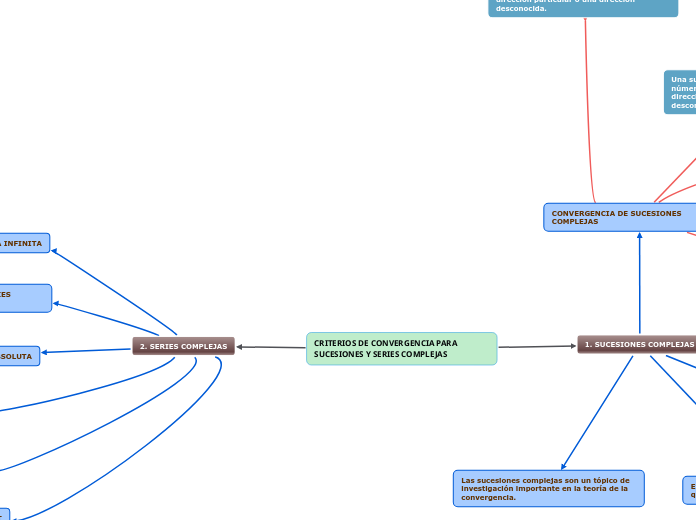
CRITERIOS DE CONVERGENCIA PARA SUCESIONES Y SERIES COMPLEJAS

もっと見る

La convergencia cultural- Octavio Islas

Maria Alejandra Hernandezにより

CARTILLA DE CLASIFICACIÓN DOCUMENTAL

Jennifer Hernándezにより

Impacto de la convergencia de medios en la educación

dayana mendozaにより

CONVERGENCIA DIGITAL AGENCIA ENGINE

Miguel Olanoにより

CRITERIOS DE CONVERGENCIA PARA SUCESIONES Y SERIES COMPLEJAS

1. SUCESIONES COMPLEJAS

CONVERGENCIA DE SUCESIONES COMPLEJAS

El número natural N indica el punto de inicio en el que se empieza a aplicar el umbral ε.

El valor ε se refiere a un umbral, por debajo del cual se considera que la sucesión converge.

Esto significa que si la distancia entre los dos es menor que un cierto valor ε, entonces la sucesión se dice que converge a ese número.

La convergencia de una sucesión compleja a un número complejo se determina por la distancia entre la sucesión y el valor de convergencia.

Una sucesión compleja es una secuencia de números complejos que puede tener una dirección particular o una dirección desconocida.

Estudiar la convergencia de sucesiones complejas implica evaluar la variación de los elementos de la secuencia y las relaciones entre ellos.

Existen varios criterios de convergencia para sucesiones complejas, cada uno con sus propias características y limitaciones.

Estos criterios permiten identificar cuando una sucesión convergerá hacia un límite determinado o no.

Los criterios de convergencia para sucesiones complejas son esenciales para comprender y analizar el comportamiento de estas sucesiones.

Existen varias definiciones de convergencia que se aplican a las sucesiones complejas.

Estudiar el comportamiento de las sucesiones complejas es una tarea desafiante debido a la complejidad matemática de los conceptos involucrados.

Las sucesiones complejas son un tópico de investigación importante en la teoría de la convergencia.

2. SERIES COMPLEJAS

CRITERIO DE DIRICHLET

SI UNA SERIE COMPLEJA Σ A_N CONVERGE Y {B_N} ES UNA SUCESIÓN DE NÚMEROS COMPLEJOS ACOTADA (ES DECIR, EXISTE M TAL QUE |B_N| ≤ M PARA TODO N) Y MONÓTONA DECRECIENTE (|B_N+1| ≤ |B_N| PARA TODO N), ENTONCES Σ A_N * B_N CONVERGE

CRITERIO DE LA RAZÓN

DADA UNA SERIE COMPLEJA Σ C_N, SI EXISTE UN LÍMITE L TAL QUE LIM |C_{N+1}/C_N| = L, ENTONCES LA SERIE CONVERGE SI L 1

CRITERIO DE COMPARACIÓN

SI Σ A_N Y Σ B_N SON DOS SERIES COMPLEJAS CON A_N Y B_N NÚMEROS COMPLEJOS, Y |A_N| ≤ |B_N| PARA TODO N, ENTONCES SI Σ B_N CONVERGE, Σ A_N TAMBIÉN CONVERGE

CRITERIO DE CONVERGENCIA ABSOLUTA

UNA SERIE COMPLEJA Σ C_N SE DICE QUE CONVERGE ABSOLUTAMENTE SI Σ |C_N| CONVERGE

CRITERIO DE CAUCHY PARA SERIES COMPLEJAS

UNA SERIE COMPLEJA Σ C_N CONVERGE SI Y SOLO SI PARA CUALQUIER Ε > 0, EXISTE UN NÚMERO NATURAL N TAL QUE PARA TODO M > N ≥ N, |C_N + C_{N+1} + ... + C_M| < Ε

SERIE COMPLEJA INFINITA

UNA SERIE COMPLEJA ES UNA SUMA INFINITA DE TÉRMINOS COMPLEJOS