によって Kim Kim 2年前.
1030
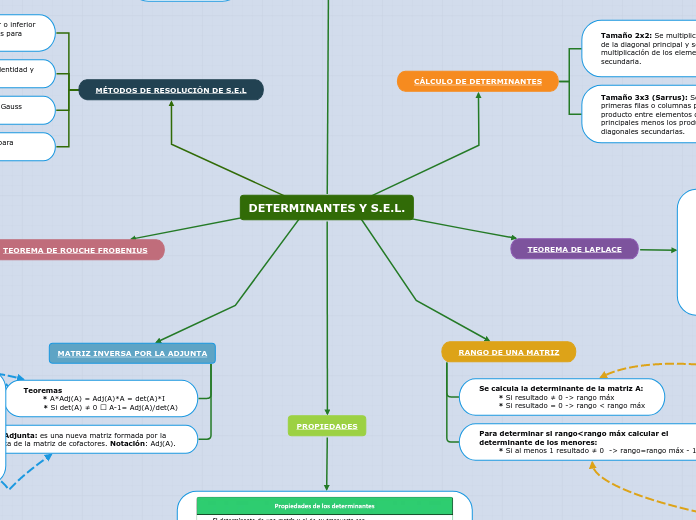
DETERMINANTES Y S.E.L.
によって Kim Kim 2年前.
1030

もっと見る
Si # de inversiones es impar: permutación impar y (-)
Si # de inversiones es par: permutación par y (+)