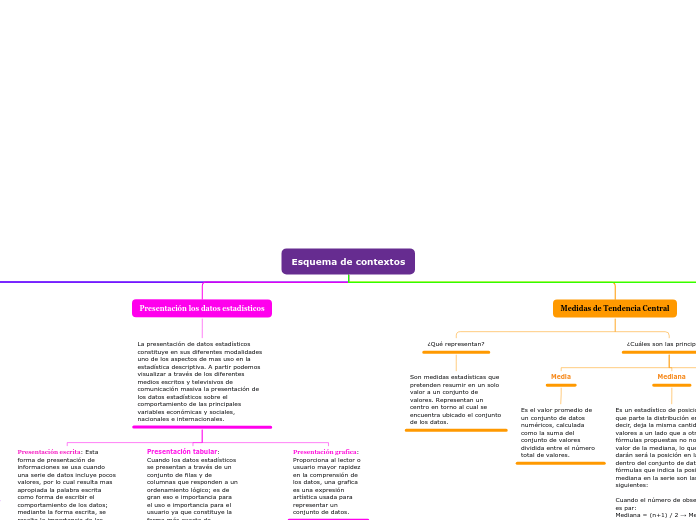
Esquema de contextos
Aplicaciones de la estadística en el Campo Empresarial
-El control de calidad.
-El nivel de averías y las frecuencias.
-Los tiempos para cambios o preparación de herramientas.
-Los niveles de productividad de distintos procesos, actividades y productos.
Probabilidad
Es simplemente qué tan posible es que ocurra un evento determinado. Cuando no estamos seguros del resultado de un evento, podemos hablar de la probabilidad de ciertos resultados: qué tan común es que ocurran. Al análisis de los eventos gobernados por la probabilidad se le llama estadística.
Medidas de Variabilidad
Coeficiente de variación
Su cálculo se obtiene de dividir la desviación típica entre el valor absoluto de la media del conjunto y por lo general se expresa en porcentaje para su mejor comprensión. X → Variable sobre la que se pretenden calcular la varianza
σx → Desviación típica de la variable X.
| x̄ | → Es la media de la variable X en valor absoluto con x̄ ≠ 0
Desviación Típica
Es otra medida que ofrece información de la dispersión respecto a la media. Su cálculo es exactamente el mismo que la varianza, pero realizando la raíz cuadrada de su resultado. Es decir, la desviación típica es la raíz cuadrada de la varianza. X → Variable sobre la que se pretenden calcular la varianza
xi → Observación número i de la variable X. i puede tomará valores entre 1 y n.
N → Número de observaciones.
x̄ → Es la media de la variable X.
Varianza
Es una medida de dispersión que representa la variabilidad de una serie de datos respecto a su media. Formalmente se calcula como la suma de los residuos al cuadrado divididos entre el total de observaciones. X → Variable sobre la que se pretenden calcular la varianza
xi → Observación número i de la variable X. i puede tomará valores entre 1 y n.
N → Número de observaciones.
x̄ → Es la media de la variable X.
Rango
Es un valor numérico que indica la diferencia entre el valor máximo y el mínimo de una población o muestra estadística. Su fórmula es: R = Máxx – Mínx
Donde:
R → Es el rango.
Máx → Es el valor máximo de la muestra o población.
Mín → Es el valor mínimo de la muestra o población estadística.
x → Es la variable sobre la que se pretende calcular esta medida.
¿Qué representa?
Nos determina el grado de acercamiento o distanciamiento de los valores de una distribución frente a su promedio de localización, indicando por medio de un número si las diferentes puntuaciones de una variable están muy alejadas de la media.
Medidas de Tendencia Central
¿Cuáles son las principales?
Moda
La moda es el valor que más se repite en una muestra estadística o población. No tiene fórmula en sí mismo. Lo que habría que realizar es la suma de las repeticiones de cada valor.
Mediana
Es un estadístico de posición central que parte la distribución en dos, es decir, deja la misma cantidad de valores a un lado que a otro. Las fórmulas propuestas no nos darán el valor de la mediana, lo que nos darán será la posición en la que está dentro del conjunto de datos. Las fórmulas que indica la posición de la mediana en la serie son las siguientes:
Cuando el número de observaciones es par:
Mediana = (n+1) / 2 → Media de las posiciones observaciones
Cuando el número de observaciones es impar:
Mediana = (n+1) / 2 → Valor de la observación
Media
Es el valor promedio de un conjunto de datos numéricos, calculada como la suma del conjunto de valores dividida entre el número total de valores.
¿Qué representan?
Son medidas estadísticas que pretenden resumir en un solo valor a un conjunto de valores. Representan un centro en torno al cual se encuentra ubicado el conjunto de los datos.
Presentación los datos estadísticos
La presentación de datos estadísticos constituye en sus diferentes modalidades uno de los aspectos de mas uso en la estadística descriptiva. A partir podemos visualizar a través de los diferentes medios escritos y televisivos de comunicación masiva la presentación de los datos estadísticos sobre el comportamiento de las principales variables económicas y sociales, nacionales e internacionales.
Presentación grafica: Proporciona al lector o usuario mayor rapidez en la comprensión de los datos, una grafica es una expresión artística usada para representar un conjunto de datos.
De acuerdo al tipo de variable que vamos a representar, las principales graficas son las siguientes:
-Histograma: Es un conjunto de barras o rectángulos unidos uno de otro, en razón de que lo utilizamos para representar variables continuas.
-Polígono de frecuencias: Esta grafica se usa para representar los puntos medios de clase en una distribución de frecuencias
-Gráfica de barras: Es un conjunto de rectángulos o barras separadas una de la otra, en razón de que se usa para representar variables discretas; las barras deben ser de igual base o ancho y separadas a igual distancia. Pueden disponerse en forma vertical y horizontal.
-Gráfica lineal: Son usadas principalmente para representar datos clasificados por cantidad o tiempo; o sea, se usan para representar series de tiempo o cronológicas.
Presentación tabular: Cuando los datos estadísticos se presentan a través de un conjunto de filas y de columnas que responden a un ordenamiento lógico; es de gran eso e importancia para el uso e importancia para el usuario ya que constituye la forma más exacta de presentar las informaciones.
Una tabla consta de varias partes, las principales son las siguientes:
-Titulo: Es la parte más importante del cuadro y sirve para describir todo él contenido de este.
-Encabezados: Son los diferentes subtítulos que se colocan en la parte superior de cada columna.
-Columna matriz: Es la columna principal del cuadro.
-Cuerpo: El cuerpo contiene todas las informaciones numéricas que aparecen en la tabla.
-Fuente: La fuente de los datos contenidos en la tabla indica la procedencia de estos.
-Notas al pie: Son usadas para hacer algunas aclaraciones sobre aspectos que aparecen en la tabla o cuadro y que no han sido explicados en otras partes.
Presentación escrita: Esta forma de presentación de informaciones se usa cuando una serie de datos incluye pocos valores, por lo cual resulta mas apropiada la palabra escrita como forma de escribir el comportamiento de los datos; mediante la forma escrita, se resalta la importancia de las informaciones principales.
Población
Una población estadística es el total de individuos o conjunto de ellos que presentan o podrían presentar el rasgo característico que se desea estudiar.
Muestra
Una muestra estadística es un subconjunto de datos perteneciente a una población de datos. Estadísticamente hablando, debe estar constituido por un cierto número de observaciones que representen adecuadamente el total de los datos.
Tipos de población
Población Infinita: Se trata de aquella población que no tiene fin. Por ejemplo la cantidad de peces en el mar.
Población Finita: es aquella en la que el numero de valores que la componen tienen un fin. Por ejemplo, la población estadística que nos indica la cantidad de arboles de una ciudad es finita, tiene un fin.
Variable
Es una propiedad característica de la población en estudio, susceptible de tomar diferentes valores, los cuales se pueden observar y medir.
Se clasifica en
V. Cuantitativa: son aquellas que tienen valor numérico como la edad, el precio de un producto, ingresos anuales de un consumidor, etc.
A su vez, las variables cuantitativas pueden ser:
-Discretas: estas son aquellas que sólo pueden tomar valores enteros como 1, 2, 8, -4, etc. En este sentido, los hermano en una familia podrán ser: 1, 2, 3..., etc. Sin embargo, nunca podrán ser 1.5 o 2.3.
-Continuas: son aquellas que pueden tomar cualquier valor real dentro de un intervalo o rango. Por ejemplo, los litros de leche ordeñados podrán se 1.5 o 10.3 etc.
V. Cualitativas: son aquellas que no se pueden medir numéricamente ejemplo: nacionalidad, color de la piel, sexo, etc. A su vez, las variables cualitativas pueden ser:
-Nominales: son datos que corresponden a categorías que por su naturaleza no admiten un orden. Por ejemplo: sexo (masculino y femenino); carrera de estudio: economía, contabilidad, administración, etc.
-Ordinales: son aquellos que corresponden a evaluaciones subjetivas que se pueden ordenar o jerarquizar. Por ejemplo: en una competencia artística las posiciones de los ganadores se ordenan o jerarquizan en primer lugar, segundo lugar, tercer lugar, cuarto lugar, etc
Definición del ciclo contable
Recolección de soportes y elaboración de libros
1. soportes internos 2. soportes externos
2. codificación de soportes internos
3.comprobante de contabilidad
4.Libro diario 4.Libros auxiliares
4.Libro mayor y balances 4.control de existencias
2.estado de situación financiera de comprobación de
saldos.
Fundamentos del ciclo contable
Reconocimiento de las políticas contables Conocimiento de los requerimientos 1. Reconocimiento facial 4. Baja de cuentas 2. Medición inicial 5. Presentación 3. Medición posterior 6. Revelación