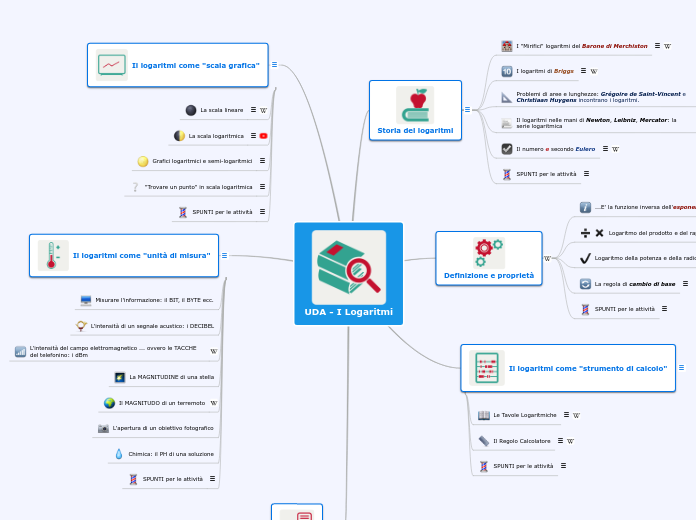
UDA - I Logaritmi
QUIZ!
Verifica finale con un quiz a risposte sia chiuse che aperte.
Strumento: Google Moduli
Il logaritmi come "unità di misura"
Alcune unità di misura sono intrinsecamente di tipo logaritmico.
Questo rende più pratico l'uso dei valori, che altrimenti sarebbero numeri estremamente grandi o estremamente piccoli.
Gli studenti raccolgono link (volutamente assenti nella mappa) e informazioni di base su ognuna delle unità di misura citate nella mappa.
Approfondiscono il significato di una unità di misura logaritmica che interviene in una materia specialistica del loro corso di studi.
Realizzano delle esperienze di misura, raccolta dati, stesura di tabelle, elaborazione di grafici sotto il coordinamento del docente della materia specialistica.
Chimica: il PH di una soluzione
L'apertura di un obiettivo fotografico
Il MAGNITUDO di un terremoto
La MAGNITUDINE di una stella
L'intensità del campo elettromagnetico ... ovvero le TACCHE del telefonino: i dBm
L'intensità di un segnale acustico: i DECIBEL
Misurare l'informazione: il BIT, il BYTE ecc.
Il logaritmi come "scala grafica"
Nella scienza e nella tecnica occorre talvolta rappresentare su un asse valori che coprono diversi ordini di grandezza. Ad esempio: 1, 10, 100, 1000.
La scala lineare in questi casi non è adeguata.
Scale basate sui logaritmi forniscono la soluzione.
Gli studenti sono invitati a raccogliere e commentare esempi di grafici in scala lineare, semilogaritmica e logaritmica, realizzando degli elaborati illustrativi di tipo grafico e testuale.
"Trovare un punto" in scala logaritmica
Le proprietà dei logaritmi stabiliscono con esattezza il valore di ogni punto preso su un asse logaritmico, una volta stabilita la posizione di due valori, ad esempio 1 e 10.
Come per la scala lineare, non ci sono margini di ambiguità.
Grafici logaritmici e semi-logaritmici
Un grafico è in scala logaritmica se ambedue gli assi (ascisse ed ordinate) sono in scala logaritmica.
E' in scala semi-logaritmica se uno dei due assi è logaritmico e l'altro è lineare.
La scala logaritmica
Lungo un asse in scala logaritmica lo stesso spostamento corrisponde alla moltiplicazione per uno stesso fattore della variabile.
La scala lineare
Ordinariamente un grafico è tracciato in scala lineare: lo stesso spostamento lungo un asse corrisponde alla stessa variazione della variabile.
Il logaritmi come "strumento di calcolo"
Dalle origini fino a tempi non lontani (anni '70) i logaritmi avevano una importanza pratica nella facilitazione dei calcoli manuali.
Con l'avvento degli strumenti di calcolo digitale questi aspetti sono divenuti esclusivamente di interesse storico.
Gli studenti realizzano un semplice regolo calcolatore in cartone o legno o plastica.
Il Regolo Calcolatore
Un REGOLO CALCOLATORE è uno strumento meccanico formato da due scale graduate "logaritmicamente" che scorrono l'una sull'altra.
La loro posizione reciproca permette di effettuare meccanicamente una moltiplicazione.
Fonte
https://it.wikipedia.org/wiki/Regolo_calcolatore
Le Tavole Logaritmiche
Una TAVOLA LOGARITMICA è un volume stampato che elenca i valori dei logaritmi di una serie di numeri consecutivi, con una certa precisione (ad es. dieci cifre decimali).
Usando una tavola e le proprietà dei logaritmi le moltiplicazioni, divisioni, potenze e radici risultano molto facilitate.
Fonte
https://en.wikipedia.org/wiki/Mathematical_table
Definizione e proprietà
Gli studenti organizzano tavole grafiche con le proprietà dei logaritmi.
Illustrano esempi con numeri semplici.
Acquisiscono abilità nell'editing al computer di formule matematiche.
La regola di cambio di base
Il logaritmo in una base è proporzionale al logaritmo in un'altra base...
Logaritmo della potenza e della radice
Si può portare fuori dal logaritmo l'esponente di una potenza...
Logaritmo del prodotto e del rapporto
Il logaritmo trasforma prodotti in somme e rapporti in differenze....
...E' la funzione inversa dell'esponenziale!
Se
ax=y
allora diciamo che
x=logay
Fonte
https://it.wikipedia.org/wiki/Logaritmo
Storia dei logaritmi
...
SPUNTI per le attività
Gli studenti eseguono ricerche di gruppo sui personaggio citati.
Inquadrano lo stato delle discipline matematiche del periodo di interesse.
Raccolgono le informazioni in elaborati multimediali.
Il numero e secondo Eulero
Leonhard Euler indica con la lettera e la base dei logaritmi naturali, definita come
e=limn→∞(1+n1)n
Questa simbologia, come molte altre introdotte dal matematico svizzero, rimarrà standard.
Fonte
https://it.wikipedia.org/wiki/E_(costante_matematica)
Il logaritmi nelle mani di Newton, Leibniz, Mercator: la serie logaritmica
Con l'invenzione dell'analisi da parte di Newton e Leibniz vengono dati gli sviluppi in serie delle funzioni elementari.
Talvolta si "riscoprono" serie già note come la serie di James Gregory per il numero pi-greco e la serie logaritmica trovata da Mercator.
Fonti
https://it.wikipedia.org/wiki/Formula_di_Leibniz_per_pi
https://it.wikipedia.org/wiki/Serie_di_Mercator
Problemi di aree e lunghezze: Grégoire de Saint-Vincent e Christiaan Huygens incontrano i logaritmi.
Il gesuita fiammingo Grégoire de Saint-Vincent riconosce la natura logaritmica dell'area sottesa dall'iperbole equilatera.
Poco dopo l'olandese Christiaan Huygens nota che il problema della rettificazione della parabola si riconduce alla quadratura dell'iperbole. Anche la lunghezza dell'arco di parabola è, quindi, di natura logaritmica.
Fonte
Carl Boyer, Storia della Matematica, Mondadori.
I logaritmi di Briggs
Henry Briggs, venuto a conoscenza dei logaritmi di Nepero, sostiene l'uso della base 10.
Stende le prime tavole logaritmiche in questa base.
Fonte
https://it.wikipedia.org/wiki/Henry_Briggs
I "Mirifici" logaritmi del Barone di Merchiston
John Napier, nobiluomo scozzese che si diletta di matematica, propone nel 1614 i suoi logaritmi come strumento per facilitare le moltiplicazioni.
Fonte
https://it.wikipedia.org/wiki/Nepero