IO2 TAREA SEMANA 2

もっと見る

Teoría de la Autopoiésis

Gonzalo .により

ENFOQUES PEDAGOGICOS Y DIDACTICAS CONTEMPORANEAS

Angelica Mencoにより

TEORÍAS QUE SUSTENTAN EL DESARROLLO SOCIO AFECTIVO EN LA INFANCIA

Karla Aguilarにより

SISTEMA ERGONOMICO Y FACTORES DETERMINANTES

angie carolina torres camargoにより

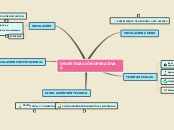
INVESTIGACIÓN OPERATIVA 2

SIMULACIÓN MONTECARLO

COMO AGRUPAR INFORMACIÓN: INTERVALOS

FRECUENCIA ACUMULADA

Número de observaciones con un valor inferior o igual al rango.

FRECUENCIA RELATIVA

Frecuencia dividida entre el total de observaciones

FRECUENCIA

Número de observaciones que se repiten dentro de un rango

INTERVALO

Característica que se usa para dividir las observaciones

DEFINICIÓN Y CONCEPTOS

Utiliza los números aleatorios para hacer la simulación

Sirve cuando hay dos o más variables que se comportan de manera independiente

Es un método no determinista o estadístico numérico, usado para aproximar expresiones matemáticas complejas y costosas de evaluar con exactitud

SIMULACIÓN COMPUTACIONAL

PRECAUCIONES

Por si misma, la Simulación, no resuelve los problemas

Es difícil verificar si los resultados son válidos

Por lo general son ignorados los factores humanos y tecnológicos

Los resultados pueden ser mal interpretados

Algunas veces soluciones mejores y más fáciles son pasadas por alto

Puede ser costosa y consumidora de tiempo inicialmente

VENTAJAS

Permite Modelar la Incertidumbre y procesos estocásticos

Flexibilidad para modelar las cosas tal como son

Conocer oportunamente hechos relevantes

Asegurar que el sistema se comportará como se desea

Reducir el tiempo de desarrollo del sistema

Disminuir inversiones y gastos de operación

Mejorar desempeño del sistema

Permite manejar procesos no homogéneos

Un Método para Estudiar un amplio abanico de modelos de sistemas del mundo real

Uso de software para “imitar” las operaciones y características del sistema, a menudo en el tiempo

Uso de evaluación numérica con el computador

SIMULACIÓN

SISTEMAS

TIPOS DE SISTEMAS

COMPLEJOS

Es imposible modelarlos de manera exacta

IDEAL

LÓGICOS

MATEMÁTICOS

Conjunto de elementos dinámicamente relacionados formando una actividad para alcanzar algún objetivo. Operando sobredatos, energía y/materia para proveer información

Se refiere a un gran conjunto de métodos y aplicaciones que buscan imitar el comportamiento de los sistemas reales

CAMPOS DE APLICACIÓN

SISTEMAS 911

BANCOS

SUPERMERCADOS

INGENIERÍA

RESTAURANTES

QUIMICA

MEDICINA

TEORÍA DE COLAS

Elementos existentes

El proceso de servicio

Cola

Redes de colas

Mecanismo de servicio

Disciplina de la cola

Capacidad de la cola

Cliente

Fuente de entrada o población potencial

Objetivos

Prestar atención al tiempo de permanencia en el sistema o en la cola de espera

Establecer un balance equilibrado (“óptimo”) entre las consideraciones cuantitativas de costes y las cualitativas de servicio

Evaluar el impacto que las posibles alternativas de modificación de la capacidad del sistema tendrían en el coste total del mismo

Identificar el nivel óptimo de capacidad del sistema que minimiza el coste del mismo

Agner Krarup Erlang,

Es el estudio matemático de las colas o líneas de espera dentro de un sistema.

SIMULACIÓN A MANO

EXPERIMENTO DE GEORGES LOUIS LECLREC

Reducción de la varianza

Lanzando la aguja hasta que el error del estimado es suficientemente pequeño

Usó muestreo secuencial para controlar el errorjmzxln

Experimento lanzando una aguja en una mesa con líneas marcadas para determinar el valor de pi

1733