によって Laura cAMILA 5年前.
696
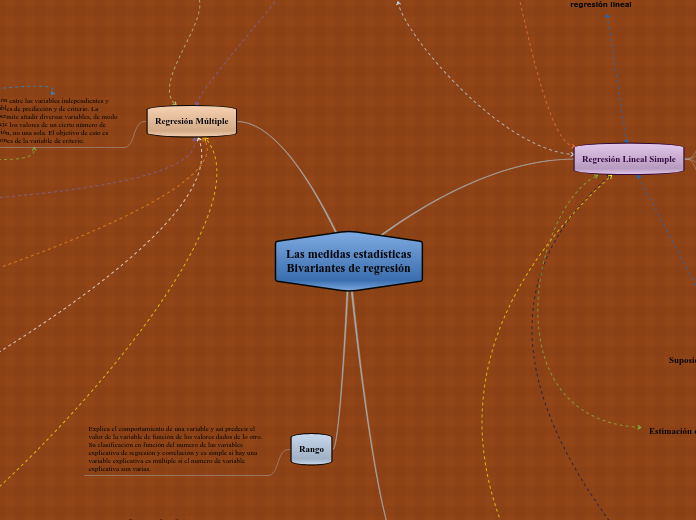
Las medidas estadísticas Bivariantes de regresión
によって Laura cAMILA 5年前.
696

もっと見る
donde: b0 : es el valor que representa (estimador) a ß0 b1 : es el valor que representa (estimador) a ß1 SPXY : denota a la suma de productos de X con Y, SCX : denota a la suma de cuadrados de X.