によって Omar Manning 4年前.
302
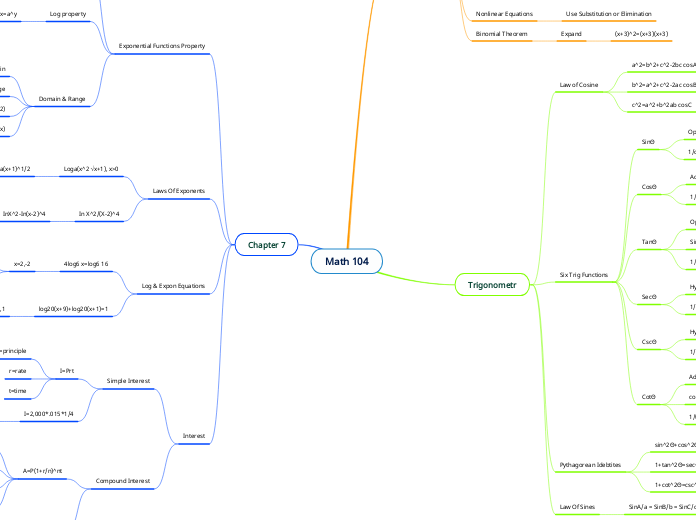
Math 104
によって Omar Manning 4年前.
302

もっと見る
A=2,000(1+(0.015/4)^4*1
A=$2030.17
A=P(1+r/n)^nt
n=times it compound
I=2,000*.015*1/4
I=$2038.17
I=Prt
t=time
r=rate
P=principle
X=-1,1
Final answer: x=1
x=2,-2
Final Answer: x=2
"x cant be negative"
InX^2-In(x-2)^4
"Express all powers as factors"
2Inx-4In(x-2)
2logax+loga(x+1)^1/2
"Express All powers as factors"
All powers= Exponents
2logax+1/2loga(x+1)
g(x)=log(5+x/5-x)
Interval Notation: (-5,5)
f(x)=log3(x+2)
Domain: {x|X>-2}
Interval Notation: (-2,∞)
Range
(∞,∞)
Domain
(0,∞)
Cant have zero so its not included
y=logx ↔ x=a^y
log3 81 ↔ y=log3 81
y=4
e^u=25 ↔ u=loge25
1.6^3= ↔ 3=log1.6
y=log7x ↔ x=7^y
1/tanΘ
cosΘ/sinΘ
Adjacent/Opposite
1/sinΘ
Hypotenuse/Opposite
1/cosΘ
Hypotenuse/Adjacent
1/cotΘ
SinΘ/cosΘ
Opposite/Adjacent
1/secΘ
Adjacent/ Hypotenuse
1/cscΘ
Opposite/Hypotenuse
(x+3)^2=(x+3)(x+3)
3x3 Determinants
2x2 Determinats