variabilidad estudia o determina las distintas formas de la distribución, de acuerdo con el fin perseguido por el investigador o estudiante de Estadística.
Medidas de dispersión o de variabilidad
medidas de variabilidad más comunes: • El rango (amplitud o recorrido). • La desviación absoluta promedio. • La varianza. • La desviación estándar. • La dispersión relativa: el coeficiente de variación.
COEFICIENTE DE VARIACION
El coeficiente de variación (CV) es la medida relativa que permite darnos una idea ge- neral de la magnitud de la desviación estándar en relación con la magnitud de la media aritmética.
matemáticamente se expresa: CV=[O/ μ] (100) CV=[S/x̄](100)
Coeficiente de variación es la medida de variabilidad que se utiliza principalmente para: 1. Comparar la variabilidad entre dos grupos de datos que tengan la misma unidad de medida, o bien, distinta. 2. Comparar el comportamiento de dos grupos de datos obtenidos por dos o más personas distintas. 3. Comparar dos grupos de datos que tienen distinta media aritmética. 4. Determinar si cierta media aritmética es consistente con cierta varianza
LA DESVIACION ESTANDAR
La desviación estándar es la medida de dispersión promedio más importante. Debido a la dificultad de poder medir con la varianza el grado de dispersión en un conjunto de datos, se puede crear este nuevo estadístico que es igual a la raíz cuadrada positiva de la varianza; es decir, en la desviación estándar, las unidades con que se mide este nuevo estadístico de dispersión serán las mismas que tienen las observaciones y la media aritmética de éstas.
S=√nΣi-1(xi-x̄)ʌ2/n1=√nΣi(di)ʌ2/n-1 O=√nΣi-1(xi-μ)ʌ2/n=√nΣi-1(di)ʌ2/n
donde: x i=observación i en la muestra o en la población. x̄ = media aritmética de la muestra. µ=media aritmética de la población. n=número total de datos en la muestra. N=número total de datos en la población. di=desviaciones de cada observación con respecto a la media muestral o a la media poblacional, respectivamente.
LA VARIANZA
Ésta es un estadístico que se define como el promedio de las desviaciones con respecto a la media, elevadas al cuadrado, y es similar a la desviación absoluta promedio; sin embargo, en este caso se elimina el uso del valor absoluto y se reemplaza por otra alternativa matemática que consiste en elevar al cuadrado todas las desviaciones, esto da como resultado que todas éstas sean ahora positivas, lo que evita el uso del valor absoluto.
La varianza se simboliza matemáticamente con la letra griega s2 (sigma al cuadrado) para la población, y s2 para el caso de una muestra. Matemáticamente, la varianza se calcula para una muestra mediante la relación siguiente:
σ² = ( Σ (x-μ)² ) / N.
DESVIACION ABSOLUTA PROMEDIO
Es una medida de dispersión promedio o desviación promedio, y es igual a la sumatoria de los valores absolutos de las desviaciones entre el total de datos. Las desviaciones se definen como la diferencia entre cada uno de los datos en el conjunto de estudio y el estadístico de tendencia central usado (media aritmética o mediana).
define matemáticamente como: DAP=n∑i=1[xi-x]/n=n∑i=1[di]/n
donde: DAP=desviación absoluta promedio. [di]=[x1-x] valores absolutos de las desviaciones de cada dato x1 con respecto a la media aritmética. n=número de datos en el conjunto.
RANGO,AMPLITUD O RECORRIDO
El rango se clasifica como una medida de distancia. El recorrido se puede conocer con facilidad a partir de una muestra ordenada de tamaño n, en donde el rango o recorrido es la diferencia que hay entre el valor máximo y el valor mínimo. Matemáticamente, el rango se define como: R=Dma-Dme
donde: R=Recorrido Dma=dato de mayor valor en el conjunto de datos. Dme=dato de menor valor en el conjunto de datos. Esta medida de variabilidad es muy útil cuando sólo se quiere conocer la diferencia entre los datos extremos de un conjunto.
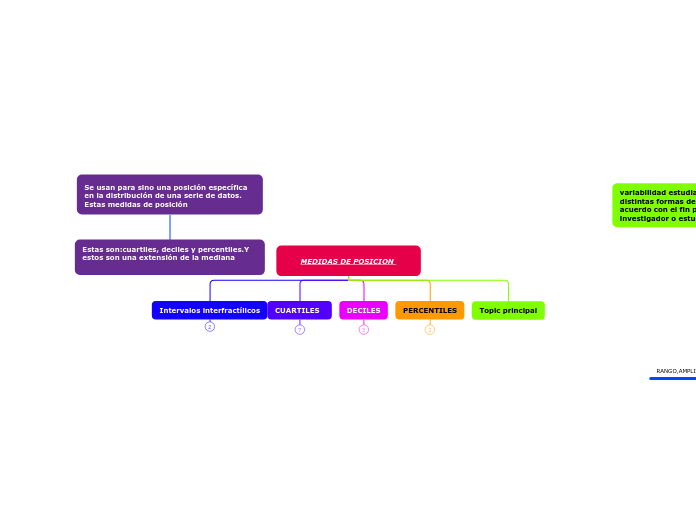
Se usan para sino una posición específica en la distribución de una serie de datos. Estas medidas de posición
Estas son:cuartiles, deciles y percentiles.Y estos son una extensión de la mediana
MEDIDAS DE POSICION
Topic principal
PERCENTILES
Es una medida estadística que se usa mucho cuando se quiere clasificar o ubicar carac- terísticas en las personas (peso, estatura, etc.). Estas medidas son números que dividen una sucesión de datos ordenados en cien partes porcentualmente iguales.
Si los datos se encuentran agrupados en una tabla de frecuencias, entonces los percentiles se calculan mediante la fórmula: Pk=Lk+[k(n/100)-Fk/fk] (T) donde: k=1, 2, 3, 4, 5, 6, 7, ..., 99 el número de percentil a calcular. Lk=límite real inferior de la clase que contiene el percentil k. n=La clase del percentil k se determina de manera similar que en el caso de la mediana: (k(n/100)) número de datos. Fk=frecuencia acumulada de la clase que antecede a la del percentil k. ƒk=frecuencia absoluta de la clase del percentil k. T=tamaño del intervalo de la clase del percentil k.
DECILES
Los deciles son números que dividen a una serie ordenada de datos en diez partes por- centualmente iguales, y no en cuatro como en el caso de los cuartiles. Los deciles pue- den calcularse del uno (D 1 ) al decil nueve (D 9)
Dk=Lk+[k(n/10)-Fk/fk](T)
donde: k = 1, 2, 3, 4, 5, 6, 7, 8, 9 el número de decil a calcular. Lk=límite real inferior de la clase que contiene el decil k. La clase del decil k se determina de forma similar que el caso de la mediana (k(n/10). n=número de datos. Fk=frecuencia acumulada de la clase que antecede a la clase del decil k. ƒk=frecuencia absoluta de la clase del decil k. T=tamaño del intervalo de la clase del decil k.
CUARTILES
En una serie de datos ordenados, los números que dividen a la serie en cuatro partes porcentualmente iguales
Los cuartiles se utilizan en la construcción de gráficas de caja y de bigote.
Para calcular la ubicación del cuartil se deben llevar a cabo los siguientes pasos: 1. Organizar los datos en forma ascendente. 2. Calcular la posición del cuartil.
Q1 = P 25 cuando n i n=[25/100] (n) Q3 = P 75 cuando n i n=[75/100] (n)
i = ubicación del cuartil. n = número de datos de la serie. P % = porcentaje del cuartil de interés. Q k = cuartil de interés. k =número de cuartil.
uso del intervalo intercuartílico permite medir la extensión o dispersión de los datos. El rango intercuartílico es la diferencia entre el primero y el tercer cuartil. La expresión matemática para el cálculo del rango intercuartílico es:
Rango intercuartílico =Q 3 - Q 1 2.17
Intervalos interfractílicos
Los intervalos que miden las diferencias entre dos valores se llaman percentiles o fractiles
Cualquier valor de una serie de datos que se encuentre bajo de una proporción espe- cífica se conoce como fractil y el que esté bajo un porcentaje determinado, percentil.